
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Проектирование грп на основе унифицированного подхода
Мы окончили главу 3 тем, что обрисовали определенную логику проектирования: для данного количества проппанта, которое достигает продуктивного пласта, мы можем определить оптимальную длину (и ширину). Один из главных результатов был такой, что при низких и средних числах проппанта (относительно малые объемы проппанта и/или средние до высоких проницаемости пласта) оптимальный компромисс достигается при CfD = 1.6.
Когда проницаемость пласта выше 50 мД, практически невозможно получить число проппанта выше 0.1. Типичные числа проппанта для высокопроницаемых ГРП находятся в диапазоне от 0.0001 до 0.01. Таким образом, для пластов средней и высокой проницаемости оптимальная безразмерная проводимость трещины всегда составляет  .
.
В «плотных газовых пластах» возможно получить высокие безразмерные числа проппанта, по крайней мере в принципе. Если мы примем ограниченную площадь дренирования и не будем задаваться вопросом, попадает ли проппант в пласт на самом деле, то можно рассчитать безразмерные числа проппанта равные 1 или даже 5. Однако на практике числа проппанта больше единицы маловероятны.
Когда расклиненный объем становится очень большим, оптимальный компромисс имеет место при более высоких безразмерных проводимостях трещины просто потому, что отношение проникновения трещины не может быть больше единицы (т.е., длину трещины начинает ограничивать расстояние между скважинами или пределы пласта).
Ключевым вопросом в дизайне является принятая высота трещины. Отношение высоты трещины к мощности продуктивного пласта определяет объемную эффективность (коэффициент использования) проппанта. Фактическое число проппанта зависит от той части проппанта, которая размещена в продуктивный пласт. Оно рассчитывается как объем нагнетенного проппанта, помноженный на объемную эффективность проппанта. Поэтому, строго говоря, желаемая оптимальная длина может быть получена, только если высота трещины уже известна. В нижеследующем рассмотрении мы принимаем, что высота трещины известна. Позже мы вернемся к этому вопросу.
Время закачки
Вооруженные требуемой длиной и считая, что  ,
, 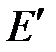 ,
, 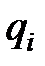 ,
,  ,
,  и
и  известны, мы можем проектировать операцию гидроразрыва пласта. Первая задача — определить время нагнетания,
известны, мы можем проектировать операцию гидроразрыва пласта. Первая задача — определить время нагнетания,  , используя комбинацию уравнения ширины и материального баланса. Первая часть типичной процедуры проектирования представлена в таблице 7-4. Отметьте, что темп нагнетания,
, используя комбинацию уравнения ширины и материального баланса. Первая часть типичной процедуры проектирования представлена в таблице 7-4. Отметьте, что темп нагнетания,  , относится к пульпе (не к чистой жидкости), нагнетаемой в одно крыло.
, относится к пульпе (не к чистой жидкости), нагнетаемой в одно крыло.
Методы, используемые для уточнения  , изложены в таблицах 7-5 по 7-7.
, изложены в таблицах 7-5 по 7-7.
Если проницаемая высота (мощность), 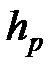 , меньше высоты трещины, то удобно использовать тот же метод, но с «кажущимися» коэффициентами утечки и мгновенной утечки. Кажущийся коэффициент утечки есть «истинный» коэффициент утечки (значение, относящееся к проницаемой части пласта), помноженный на коэффициент
, меньше высоты трещины, то удобно использовать тот же метод, но с «кажущимися» коэффициентами утечки и мгновенной утечки. Кажущийся коэффициент утечки есть «истинный» коэффициент утечки (значение, относящееся к проницаемой части пласта), помноженный на коэффициент  , определяемый как отношение проницаемой поверхности к поверхности трещины (ср. рис. 7-5 и 7-6).
, определяемый как отношение проницаемой поверхности к поверхности трещины (ср. рис. 7-5 и 7-6).
| ТАБЛИЦА 7-4. Определение времени закачки |
1. Рассчитываем ширину трещины возле скважины в конце нагнетания из уравнения PKN (или любого другого) для ширины:  (или лучше в форме для неньютоновской жидкости — показана ниже) (или лучше в форме для неньютоновской жидкости — показана ниже)
|
2. Преобразуем ширину возле скважины в среднюю ширину: 
|
| 3. Принимаем коэффициент распределения времени раскрытия трещины, KL = 1.5 (методы уточнения этого значения описаны ниже). |
4. Решаем следующее уравнение для te:  (квадратное уравнение для (квадратное уравнение для 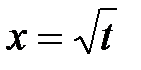 ). Выбрав ). Выбрав  в качестве новой неизвестной, можно решить простое квадратное уравнение: в качестве новой неизвестной, можно решить простое квадратное уравнение:  , где , где 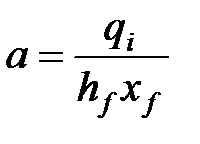 ; ;  ; ; 
|
5. Рассчитываем нагнетенный объем:  и эффективность (коэффициент использования) жидкости: и эффективность (коэффициент использования) жидкости: 
|
| ТАБЛИЦА 7-5. Уточнение KL с использованием уравнения Картера II |
Рассчитываем уточненную оценку KL из:  , где , где  и и  . Если KL достаточно близок к предыдущей прикидочной оценке, останавливаемся; в противном случае повторяем расчет материального баланса, используя новую оценку KL. . Если KL достаточно близок к предыдущей прикидочной оценке, останавливаемся; в противном случае повторяем расчет материального баланса, используя новую оценку KL.
|
| ТАБЛИЦА 7-6. Уточнение KL посредством линейной интерполяции согласно Нольте |
Рассчитываем следующее значение KL из уравнения  , где , где  . Если коэффициент KL достаточно близок к предыдущей прикидочной оценке, останавливаемся; в противном случае делаем следующую итерацию, повторяя расчет материального баланса с использованием новой оценки KL. . Если коэффициент KL достаточно близок к предыдущей прикидочной оценке, останавливаемся; в противном случае делаем следующую итерацию, повторяя расчет материального баланса с использованием новой оценки KL.
|
| ТАБЛИЦА 7-7. KL по методу a |
Принимаем значение показателя степени a для степенного закона (Таблица 7-2) рассчитываем  , используя уравнение 7-1. Используем полученное значение KL вместо 1.5 в материальном балансе. (Отметьте, что это процесс не итеративный.) , используя уравнение 7-1. Используем полученное значение KL вместо 1.5 в материальном балансе. (Отметьте, что это процесс не итеративный.)
|
Для типов геометрии PKN KGD и этот коэффициент есть отношение проницаемой высоты к высоте трещины,
 , (7-14)
, (7-14)
тогда как для радиальной модели он задается выражением
 где
где  (7-15)
(7-15)

Рис. 7-5. Отношение проницаемой площади к общей площади трещины, геометрия KGD и PKN.

РИС. 7-6. Отношение проницаемой площади к общей площади трещины, радиальная геометрия
Имеется несколько способов включить неньютоновское поведение жидкостей в уравнения для ширины. Удобная процедура — это добавить одно дополнительное уравнение, связывающее эквивалентную ньютоновскую вязкость с расходом жидкости. Приняв, что жидкость подчиняется степенному закону, можно рассчитать эквивалентную ньютоновскую вязкость для среднего поперечного сечения, использовав соответствующее уравнение из таблицы 4-3. Подставив эквивалентную ньютоновскую вязкость в уравнение ширины для модели PKN, получаем
 (7-16)
(7-16)
Не нашли, что искали? Воспользуйтесь поиском: