Теория ограниченного роста

Концевое экранирование можно рассматривать как раздувание ширины трещины в то время, когда площадь грани трещины не увеличивается. Если обозначить среднюю ширину как , а площадь грани трещины (одно крыло, одна грань) как 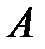, то

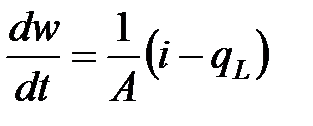(10-6)

где — темп нагнетания (для одного крыла), а 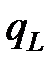— скорость утечки жидкости (из одного крыла).

Основные обозначения показаны на рис. 10-5. Приняв, что трещина радиальная с радиусом 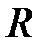, получим

(10-7)

РИС. 10-5. Радиальная геометрия трещины в высокопроницаемом ГРП.

В качестве первого приближения примем, что давление в раздувающейся трещине не зависит от местоположения (т.е., однородное). Эффективное давление, например, давление, превышающее наименьшее главное напряжение, прямо пропорционально средней ширине:

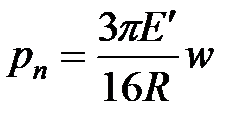(10-8)

где — модуль плоской деформации (см. главу 4).

Подставляя уравнения 10-7 и 10-8 в уравнение 10-6, получаем производную по времени от эффективного давления в виде

(10-9)

где мы опускаем нижний индекс для эффективного давления, так как производная от забойного давления и производная от эффективного давления равны.

Регистрация забойного давления и темпа нагнетания дает возможность использовать уравнение 10-9 для определения . Для этой цели необходима оценка .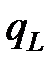

Подробности модели Картера для поглощения в пласт даны в главе 4. Приняв, что трещина удлиняется до данного момента времени согласно допущению Нольте о степенном законе, и ее удлинение останавливается в этот данный момент времени , скорость поглощения 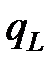сразу после этой остановки задается уравнением

(10-10)

где — текущая площадь трещины, а 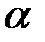— показатель степени в степенном законе роста площади. Функцию двух переменных, g -функцию, мы обсуждали в главе 4.

Для радиальной трещины, создаваемой нагнетанием ньютоновской жидкости, этот показатель степени принимается равным , а производная g -функции равна

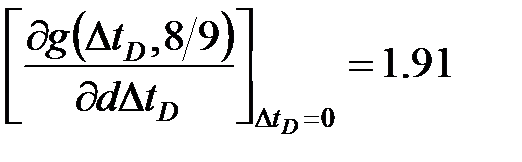(10-11)

Таким образом, получаем оценку скорости поглощения в виде

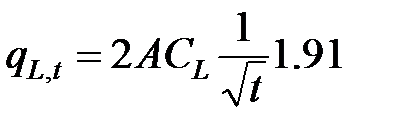(10-12)

Не нашли, что искали? Воспользуйтесь поиском: