Определение радиуса набивки, соответствующего периоду раздувания ширины

Подставив полученное выражение для скорости утечки, уравнение 10-9 можно переписать как

(10-13)

После преобразования получаем

(10-14)

Когда интервал ограниченного роста выбран, то зная угловой коэффициент и скорость нагнетания в данный момент времени 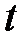, уравнение 1-14 можно решить относительно . Поскольку это кубическое уравнение, решение в явном виде дать нельзя.

Уравнение 10-14 можно использовать с фактическим темпом нагнетания пульпы, , зарегистрированным в момент времени 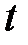, и угловым коэффициентом кривой давления в функции времени в этот конкретный момент времени. Полученное решение есть радиус набивки. На рис. 10-8 показан радиус набивки, полученный из зарегистрированных данных в этом примере данных для высокопроницаемого ГРП. Как видно из рисунка, после определенного периода нагнетания (приблизительно 25 минут) радиус набивки начинает уменьшаться. Иными словами, ближе к концу обработки «набивка» происходила только в околоскважинной части трещины. Это соответствует цели обработки, и это было достигнуто путем постепенного уменьшения темпа нагнетания на конечных этапах обработки.

РИС. 10-8. Расчетный радиус набивки с интерполяцией.

Не нашли, что искали? Воспользуйтесь поиском: