Рамалы жүйелер. Көп қабатты қаңқалы ғимараттар (9.1

Көп қабатты қаңқалы ғимараттар (9.1. а-суреті) үшін жиіліктер саны және оларға сәйкес келетін еркін көлденең тербелістер ғимарат қабаттарының санына тең болып келеді (еркіндік деңгейінің саны). Сонымен қатар жабындар мен бағаналар массасы түйіндерде жинақталған болып келеді. Көп қабатты ғимараттардың ярусты массасы мынаған тең:

m= Q/g, (9.1)

мұндағы Q – ярусты жүктемелердің уақытша жүктемелерден, қабырғалардан, бағаналардан, жабындардан пайда болуы; g – ауырлық күшінің тездетілуі.

Еркін көлденең тербеліс кезінде көп қабатты рамалардың сыртқы жүктемелері ретінде –m 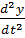. n≥6 болғанда, оларды анықталмаған жүктемелер түрінде елестетуге болады:

. (9.2)

K = - p(x) есебімен еркін тербелістердің бірқалыпты дифференциалдау теңдігін аламыз:

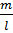
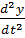- = 0. (9.3)

y=XT теңдігінің шешімінен мынадай теңдік шығады:

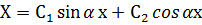, (9.4)

мұндағы: Х – еркін тербелістің ордината формасы,

Т – уақыт функциясы.

(9.5)

ω - еркін көлденең тербеліс жиілігі.

9.1.сурет. Көпқабатты қаңқалы ғимараттардың динамикалық есебін анықтау

а – көлденең рама; б – еркін көлденең тербелістің жиілігі мен формаларын анықтаған кездегі есепті схема; в – еркін тербелістің алғашқы үш формасы.

9.2.сурет. Көпқабатты рамалардағы тіректердің бойлық деформациялар есебімен еркін көлденең тербелістердің кезеңдерін анықтайды

Шеткі жағдайлар: 1) Х(0)=0;2) КХ^'(Н)=0. Сонымен қатар екі бірқалыпты теңдеу аламыз: 1) С₂=0; 2) С₁cosαН=0, есебінен cosαН=0; αН=(2і-1)π/2), мұндағы і=1,2,3... еркін тербелістің номерінің тоны.

Еркін тербеліс кезеңі (1.5) формулаға сәйкес мынадай болады:

= (9.6)

Еркін тербеліс формасы (1.4) формула бойынша анықталады.

Х= C₁sinαx = C₁sin(2i-1)πξ/2. (9.7)

Еркін тербеліс формасын анықтаған кезде алмасу қатынасын ғана міндетті түрде анықтау керек, сондықтан да (9.7) формуладағы С₁=1 болады. Еркін тербелістің алғашқы үш формасы 9.1. в-суретінде көрсетілген.

Раманың қаттылық сипаттамасы λ_fr≥ 0.7 болса, онда онда еркін тербеліс кезеңі тіректердегі деформация есебімен анықталады:

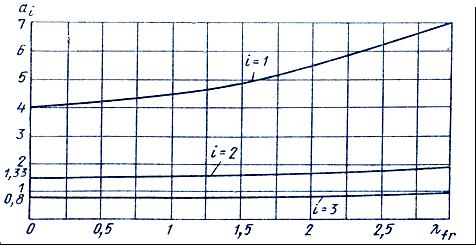
Т_і= а_i H , (9.8)

мұндағы а_i – график бойынша анықталатын коэффициент.

Не нашли, что искали? Воспользуйтесь поиском: