Теорема Остроградского-Гаусса позволяет достаточно просто рассчитать напряженность поля известной конфигурации, которое обладает каким-либо видом симметрии.

Например, если можно выбрать такую замкнутую поверхность, что линии напряженности перпендикулярны любому элементу поверхности, то, E·cos 0⁰=Е. Тогда:

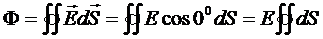
Если распределение зарядов внутри поверхности задано, то суммарный заряд также легко рассчитать. Приравняв эти два выражения друг другу, можно легко вычислить напряженность поля.

САМОСТ. III: 1.Найти поток вектора напряженности поля точечного заряда q через сферическую поверхность, центр которой совпадает с положением точечного заряда, если радиус поверхности: а)R, б) 2R.

Какова должна быть форма замкнутой поверхности, в каждой точке которой скалярное произведение вектора напряженности и нормали имеет постоянное значение, если поле создано зарядом равномерно распределенным: а) по поверхности сферы, б)по объему сферы, в) вдоль бесконечной, прямолинейной нити, г) по поверхности бесконечной плоскости.

Не нашли, что искали? Воспользуйтесь поиском: