ДИФФЕРЕНЦИАЛЬНАЯ ФОРМА ТЕОРЕМЫ ОСТРОГРАДСКОГО- ГАУССА

Пусть в некоторой области пространства известна объемная плотность зарядов r=r(x,y,z) и эта функция непрерывна аналогично представлению о непрерывном распределении вещества.

Рассмотрим в этом пространстве вблизи некоторой точки с координатами x,y,z настолько малый объем dV=dx·dy·dz, что объемная плотность зарядов в нем практически постоянна. Тогда заряд этого объема равен dq=r(x,y,z)·dV

Найдем поток через поверхность граней перпендикулярных оси ОХ:

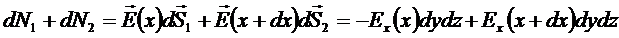
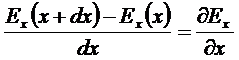
Аналогично можно рассчитать поток через две пары других оснований.

Тогда поток через поверхность всех граней объема:

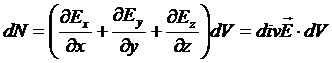
РИС.17 -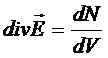

Физический смысл дивергенции вектора напряженности в том, что она равна числу линий напряженности выходящих (входящих) из единичного объема, т.е. характеризует расходимость (сходимость) линий напряженности.

Согласно теореме Остроградского-Гаусса в интегральной форме: , 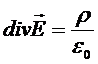- дифференциальная форма теоремы Остроградского-Гаусса.

Эта форма применима лишь при условии, если объемная плотность зарядов конечная величина, является следствием интегральной формы и констатирует, что заряды являются источниками (стоками) линий вектора напряженности.

Если ввести векторный оператор Гамильтона:

,

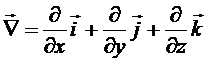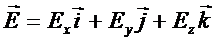
Можно записать:

Не нашли, что искали? Воспользуйтесь поиском: