Теорема о циркуляции является критерием потенциальности поля.

§8. РАЗНОСТЬ ПОТЕНЦИАЛОВ, ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ.

Как известно работа сил потенциального поля равна убыли потенциальной

энергии: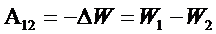

Если разделить обе части этого выражения на величину переносимого пробного заряда, то можно ввести энергетическую характеристику двух точек поля.

Разностью потенциалов между двумя точками электростатического поля называется скалярная физическая величина, численно равная работе сил поля по перемещению единичного положительного заряда между двумя этими точками.

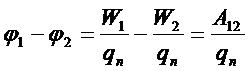
Потенциал точки поля, равный потенциальной энергии единичного положительного заряда в данной точке поля, можно определить только через потенциальную энергию в другой точке:

Если пробный заряд находится в точке 2 на очень большом расстоянии от заряда создающего поле, то они практически не взаимодействуют, так как кулоновская сила убывает обратно пропорционально квадрату расстояния.

Потенциальная энергия – энергия взаимодействия, а значит, потенциальная энергия пробного заряда в этом случае равна нулю.

Следовательно, можно принять, так называемое условие нормировки, что при r®¥ W_¥®0 и соответственно потенциал бесконечно удаленной точки поля равен нулю:

при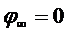

Потенциалом точки электростатического поля называется скалярная физическая величина, численно равная работе сил поля по перемещению единичного, положительного заряда из этой в бесконечно удаленную точку.

Ил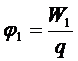и: при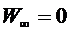

Таким образом, разность потенциалов – однозначная характеристика двух точек поля, а потенциал – неоднозначная характеристика, зависящая от условия нормировки.

Потенциал и разность потенциалов измеряются в: [j₁-j₂]=[j]=1В

Получим формулу для вычисления потенциала поля точечного заряда:

или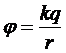

Если пробный заряд перемещается в поле, созданном несколькими точечными зарядами, то работа будет определяться силой, действующей на него со стороны результирующего поля: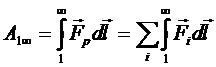

Отсюда следует принцип суперпозиции для потенциала -

потенциал точки поля, созданного несколькими точечными зарядами равен алгебраической сумме потенциалов:

Если заряд распределен по некоторому объему с объемной плотностью r=r(x,y,z), то можно найти потенциал точки поля, используя формулу для поля точечного заряда и принцип суперпозиции.

Выделим такой малый объем dV, что заряд этого объема можно считать точечным. Тогда: dq=rdV

Потенциал создаваемый этим зарядом в точке поля: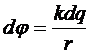

Проинтегрировав по всему объему, найдем потенциал точки поля, создаваемый всем распределенным зарядом:

Не нашли, что искали? Воспользуйтесь поиском: