СВЯЗЬ НАПРЯЖЕННОСТИ И РАЗНОСТИ ПОТЕНЦИАЛОВ.ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ.

Выразим работу сил поля через разность потенциалов А₁₂=q_n(j₁-j₂) и сравним с раннее полученной формулой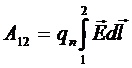

Соотношение между разностью потенциалов и напряженностью поля в интегральной форме:

Соответственно, потенциал точки поля рассчитывается по формуле:

Найдем связь между напряженностью и потенциалом в дифференциальной форме. Для поля, силы которого потенциальны:

Поле точечного заряда зависит лишь от расстояния, поэтому можно записать, что:

Тогда:

Отсюда следует, что вектор напряженности всегда направлен в сторону убывания потенциала.

Используем:

, ,

Кроме линий напряженности для изображения электростатического поля используются эквипотенциальные поверхности.

Эквипотенциальная поверхность – геометрическое место точек равного потенциала, т.е. j=const.

1) Чтобы поверхность была эквипотенциальна, необходимо и достаточно, чтобы работа по перемещению заряда между двумя любыми точками поверхности равнялась нулю.

2) Эквипотенциальная поверхность ортогональна линиям напряженности. Действительно, работа по перемещению заряда между двумя точками эквипотенциальной поверхности:

, так как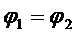

Тогда: . Это возможно, если cosa=0, т.е. a=90⁰

Например, эквипотенциальные поверхности поля отрицательного точечного заряда представляют собой сферические поверхности с центром, совпадающим с местом расположения заряда.

3)Поверхность заряженного проводника с установившимся распределением зарядов – эквипотенциальна.

На рис. 20 показаны линии напряженности и эквипотенциальные поверхности поля положительно заряженного проводника. Одна из эквипотенциальных поверхностей совпадает с его контуром

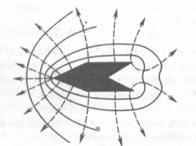
РИС.19 РИС.20

САМОСТ.IV: 1.Изобразить линии напряженности и эквипотенциальные поверхности поля:

а) положительного точечного заряда, б)двух равных точечных зарядов заряженных одноименно и разноименно,

Не нашли, что искали? Воспользуйтесь поиском: