ЭЛЕКТРИЧЕСКОЕ ПОЛЕ ЗАРЯЖЕННОГО ПРОВОДНИКА.

Любое вещество состоит, в конечном счете, из атомов. Классическая модель атома: ядро в центре и электроны, движущиеся по орбитам. Размеры ядра в 100000 раз меньше размеров атома. Электроны, по сравнению с ядром, точечные частицы. В такой модели пространство атома – область результирующего микроскопического электромагнитного поля ядра и электронов, для исследования которого не существует пробного заряда.

Макроскопическое поле вводится как усредненное микроскопическое по некоторому малому (но содержащему большое количество атомов) объему

Проводники – вещества, в которых атомы имеют один-три валентных электрона, часть которых из-за слабой связи с ядром освобождается и перемещается по всему объему проводника. Концентрация свободных электронов в n~(10²⁸-10²⁹)м^-3..

Классическая модель проводника – это в целом нейтральная система, состоящая из кристаллической решетки положительных ионов и свободных электронов, которые хаотически двигаются в поле кристаллической решетки подобно «одноатомному электронному газу».

Если проводник получил отрицательный заряд, то в течение 10^-19с происходит перераспределение свободных электронов и устанавливается такое равновесное распределение зарядов, что результирующая сила, действующая на каждый заряд, равна нулю.

Следовательно, напряженность результирующего поля внутри проводника также равна нулю. Так как: , то

Отсюда следует, что внутри проводника нет свободных избыточных зарядов. Полученный заряд располагается на поверхности проводника в слое толщиной порядка 10^-10м. Так как , то поверхность и объем проводника эквипотенциальны 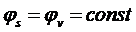_, а линии напряженности перпендикулярны поверхности проводника.

Рассмотрим, от чего зависит напряженность поля вблизи поверхности, например, положительно заряженного проводника?

Выделим настолько малый элемент поверхности DS, чтобы можно было считать его частью плоскости, а распределение зарядов на нем равномерным с поверхностной плотностью s.

В этом случае поле возле этого элемента можно считать однородным. Выберем замкнутую поверхность в виде прямого цилиндра высотой h®0 и площадью сечения равной DS (рис.26).

РИС.26 РИС.27

По теореме Остроградского поток вектора напряженности через замкнутую поверхность цилиндра: ,

Полученная величина напряженности представляет собой результат сложения напряженности двух полей: поля зарядов на выделенном элементе поверхности и поля всех остальных зарядов проводника (рис.27).

Эти вектора направлены в одну сторону вне проводника и противоположно друг другу внутри проводника. Но поле внутри проводника равно нулю. Следовательно, равны модули векторов напряженности: E_s=E₀. Тогда величина результирующей напряженности вне проводника равна: E=E_s+E₀=2E_s.

. Отсюда следует, что напряженность поля в точках вблизи заряженного элемента поверхности проводника в равных долях определяется зарядами этого элемента и всеми остальными зарядами проводника.

От чего зависит поверхностная плотность зарядов на проводнике?

Рассмотрим модель проводника, имеющего участки поверхности с различным радиусом кривизны - два проводящих шара различных радиусов, расположенных на большом (по сравнению с их радиусами) расстоянии и соединенных очень тонким проводником.

РИС.28

Если сообщить заряд любому из этих проводников, то после установления равновесного распределения зарядов, все проводники должны иметь один и тот же потенциал. Так как шары удалены на очень большое расстояние друг от друга, то можно рассчитывать их потенциал по формуле для уединенного шара: , ,

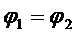
Выразим заряды шаров через поверхностную плотность зарядов ,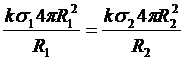

Следовательно, поверхностная плотность зарядов обратно пропорциональна радиусу кривизны поверхности проводника и чем меньше радиус кривизны, тем больше поверхностная плотность зарядов.

Поверхность проводника любой формы можно представить как множество участков сферических поверхностей с различными радиусами кривизны. Тогда плотность зарядов на поверхности заряженного проводника больше там, где меньше радиус кривизны поверхности проводника.

САМОСТ. V: 1. Электронный ветер.

2.Почему возле заостренных металлических предметов может наблюдаться свечение воздуха?

Не нашли, что искали? Воспользуйтесь поиском: