ВЕКТОР ПОЛЯРИЗАЦИИ И СВЯЗАННЫЕ ЗАРЯДЫ.

Рассмотрим плоскопараллельный слой однородного изотропного диэлектрика находящийся в однородном электрическом поле, созданном в вакууме. Пусть вектор напряженности поля составляет угол Q с нормалью. В однородном изотропном диэлектрике вектор поляризации будет направлен по вектору напряженности (рис.39).

РИС.39 РИС.40

В результате поляризации на гранях диэлектрика появятся поляризационные заряды с поверхностной плотностью:

Построим на ds цилиндр с образующими параллельными вектору напряженности. Цилиндр можно рассматривать как диполь с величиной дипольного момента:

По определению модуль вектора поляризации:

Следовательно: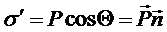

Поверхностная плотность связанных зарядов равна проекции вектора поляризации на направление нормали к поверхности диэлектрика. Физический смысл этой величины в том, что она равна величине заряда, который смещается через единичную площадку в направлении нормали к ней.

Если диэлектрик не однородный или электрическое поле не однородное, то поляризационные заряды могут появиться и внутри его объема, причем .

Рассмотрим случай диэлектрика с неполярными молекулами, хотя полученные результаты будут справедливы для всех изотропных диэлектриков. Выделим некоторый объем в диэлектрике, ограниченный поверхностью S (рис.40).

Из рис.40 видно, что через те участки поверхности, где напряженность направлена вовнутрь, часть отрицательных зарядов покинет рассматриваемый объем, а через участки, где напряженность направлена наружу, в область войдет дополнительно отрицательный заряд.

Если вошедший и вышедший заряды не равны друг другу, то внутри области

появится объемный поляризационный заряд , а на ее поверхности – поверхностный поляризационный заряд .

Введем объемную плотность поляризационных зарядов: ,

Весь заряд на поверхности можно рассчитать:

Так как диэлектрик не имел избыточного заряда, то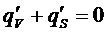

Следовательно:

Теорема Остроградского-Гаусса для вектора поляризации: поток вектора поляризации через любую замкнутую поверхность равен полному поляризационному заряду внутри этой поверхности, взятому с противоположным знаком.

В дифференциальной форме: или

Физический смысл этого выражения в том, что источниками линий вектора поляризации являются только связанные заряды.

При поляризации диэлектрика поверхностные поляризационные заряды возникают всегда, а объемные поляризационные заряды могут возникать только в неоднородных диэлектриках или в неоднородных полях.

Не нашли, что искали? Воспользуйтесь поиском: