ЭНЕРГИЯ НЕПРЕРЫВНО РАСПРЕДЕЛЕННЫХ ЗАРЯДОВ, ЭНЕРГИЯ ЗАРЯЖЕННОГО ПРОВОДНИКА, КОНДЕНСАТОРА.

Если заряды непрерывно распределены в некотором объеме с плотностью r=r(x,y,z) или с поверхностной плотностью s=s(x,y,z), то это аналогично системе точечных зарядов при n®¥.

Выделяем такие dv и ds, что соответствующие заряды можно считать точечными dq=r(x,y,z)dv dq=s(x,y,z)ds.

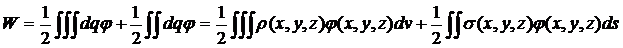Так, в общем случае, можно рассчитать энергию взаимодействия зарядов непрерывно распределенных по объему и поверхности тела. Расчет по этой формуле дает в этом случае собственную энергию взаимодействия зарядов тела.

Если по этой формуле рассчитывать энергию взаимодействия, например, двух заряженных тел, то потенциал в месте расположения каждого элементарного заряда dq будет определяться всеми зарядами обоих тел.

В этом случае энергия взаимодействия зарядов состоит из двух собственных энергий взаимодействия зарядов каждого тела и энергии взаимодействия зарядов одного тела с зарядами другого тела. W=W₁+W₂+W₁₂

ПРИМЕР 1. Найдем энергию заряженного проводника. Заряды расположены на его поверхности, а объем и поверхность эквипотенциальны, т.е. j=const. Тогда:

, где q – заряд проводника, j - потенциал проводника при условии, что j_¥=0.

Можно рассчитать энергию заряженного проводника как работу по его зарядке: A=DW=W-0=W.

Пусть проводник емкостью С заряжен и имеет соответственно некоторый потенциал потенциал j. Чтобы увеличить его заряд на dq нужно совершить работу dA=dqj по перемещению этого заряда из бесконечности. Тогда: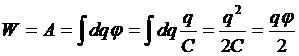

Эти формулы дают значение собственной энергии зарядов проводника.

ПРИМЕР 2. Рассчитаем энергию заряженного плоского конденсатора как работу по его зарядке.

Эти формулы определяют полную энергию взаимодействия зарядов: не только энергию взаимодействия зарядов одной обкладки с зарядами другой, но и энергию взаимодействия зарядов каждой обкладки.

Не нашли, что искали? Воспользуйтесь поиском: