ЭНЕРГИЯ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ, ЭНЕРГИЯ ВЗАИМОДЕЙСТВИЯ ЗАРЯЖЕННЫХ ТЕЛ.

Взаимодействие зарядов осуществляется посредством поля, которое, как материальный объект, должно обладать энергией.

В плоском конденсаторе, если пренебречь краевыми эффектами, однородное электрическое поле сосредоточено в пространстве между пластинами.

Выразим энергию конденсатора через напряженность поля, используя формулы:

, , ,

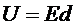Тогда: 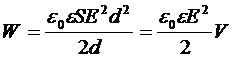, где V=Sd - объем пространства, в котором сосредоточено электрическое поле конденсатора (пренебрегая краевыми эффектами).

В этом случае величина представляет собой объемную плотность энергии электрического поля.

Важно отметить, что это свидетельствует о локализации энергии в пространстве, в котором существует электрическое поле.

Действительно, эксперименты, особенно с переменными во времени полями, которые могут существовать независимо от зарядов и распространяться в пространстве, показывают, что носителем энергии является поле.

Если электрическое поле не однородно, но существует в пространстве, заполненном изотропным диэлектриком, то можно выделить такой малый объем dV, в котором поле можно считать однородным. Тогда: ,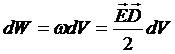

Необходимо отметить, что при создании поля в изотропном диэлектрике необходима дополнительная работа на его поляризацию в каждой единице объема, которую можно вычислить, если учесть, ч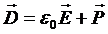то: , то .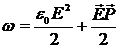

Первое слагаемое в этом выражении представляет плотность энергии поля в вакууме, тогда второе слагаемое – это работа на поляризацию единичного объема диэлектрика.

Рассмотрим систему из двух заряженных тел, создающих в пространстве электростатические поля. Согласно принципу суперпозиции, в этом случае, в каждой точке пространства результирующее поле: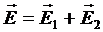

Полная энергия этой системы:

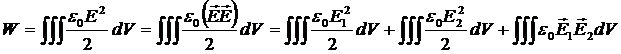
Как уже обсуждалось в предыдущем параграфе, первые два интеграла в этом выражении представляют собой собственные энергии первого и второго заряженных тел, а последний интеграл - это энергия их взаимодействия.

Анализ данной формулы позволяет сделать следующие выводы:

1.Собственная энергия каждого заряженного тела и полная энергия системы всегда положительны. Энергия взаимодействия может быть и положительной и отрицательной.

2. Если распределение зарядов на телах не изменяется при их возможных перемещениях, то собственная энергия постоянна. Изменение энергии системы определяется только изменениями энергии взаимодействия тел.

Это и происходит, если заряженные тела можно рассматривать как точечные заряды.

3. Энергия электрического поля – не аддитивная величина, т.е. энергия результирующего поля, в общем случае, не равна сумме энергий двух полей.

Представление о локализации энергии в поле позволяет не только находить величину энергии, заключенную в конкретных объемах пространства, но и рассчитывать работу против электрических сил при различных перемещениях заряженных тел:

Кроме того, если заряды на проводниках остаются постоянными, а при их медленных перемещениях можно пренебречь преобразованием электрической энергии в другие формы, то работа электрических сил совершается за счет убыли электрической энергии системы и можно рассчитать эту силу:

, ,

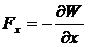где F_x – проекция искомой силы на малое перемещение вдоль оси ОХ.

Поскольку сила зависит лишь от взаимного расположения и распределения зарядов, то ее нахождение в этом случае сводится к нахождению изменения энергии при условии постоянства величины заряда.

КОЛЛОКВИУМ.

Не нашли, что искали? Воспользуйтесь поиском: