ЭКСПЕРИМЕНТАЛЬНЫЕ ЗАКОНЫ СТАЦИОНАРНОГО ТОКА.

а)ЗАКОН ОМА для участка цепи:

Если на концах проводника поддерживать разность потенциалов , то в проводнике существует электрическое поле, вызывающее направленное движение зарядов. Зависимость силы тока от приложенной разности потенциалов I=f(U) называется вольт-амперной характеристикой.

В реальных условиях вольт-амперные характеристики могут быть различными.

На рис. 56 представлены вольтамперные характеристики вакуумного диода (а), полупроводникового диода (б), металлического проводника или электролита (в).

а) б) в)

РИС.56

В последнем случае установленная экспериментальная зависимость носит название закона Ома на участке цепи: сила тока прямо пропорциональна разности потенциалов, приложенной к концам участка: 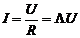, где R и L - сопротивление и проводимость проводника, соответственно. Эти величины зависят от химического состава, размеров и формы проводника, а также его температуры. 1Ом, 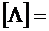1 См (Сименс).

Для металлической проволоки или однородного проводника цилиндрической формы сопротивление может быть рассчитано по формуле: , где l и S длина и сечение проволоки соответственно, - удельное сопротивление, - удельная проводимость.

Удельное сопротивление и соответственно удельная проводимость зависят от концентрации и заряда носителей тока, структуры вещества (параметров кристаллической решетки для твердых тел), температуры. 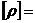1 Ом×м

Вещество Удельное сопротивление, Ом×м

Серебро 1,6×10^-8

Медь 1,7×10^-8

Алюминий 2,7×10^-8

Алмаз 1,0×10⁺¹⁰

Установлено, что для многих металлов и сплавов удельное сопротивление линейно зависит от температуры (при не слишком низких температурах): , где - удельное сопротивление при 0⁰С, -температурный коэффициент сопротивления.

Основной причиной увеличения удельного сопротивления с ростом температуры является возрастание интенсивности хаотического движения ионов кристаллической решетки. Экспериментально установлено, впервые для ртути, а затем для многих металлов и сплавов, что при температурах близких к абсолютному нулю (0,14 – 20 К) удельное сопротивление скачкообразно уменьшается до нуля.

Это явление, названное сверхпроводимостью, невозможно объяснить в рамках классической физики и поэтому рассматривается лишь на основе квантовой теории.

РИС.57 РИС.58 РИС.59

б) ЗАКОН ДЖОУЛЯ ЛЕНЦА: При протекании тока на участке цепи с сопротивлением R выделяется количество теплоты, которое можно рассчитать по экспериментальному закону Джоуля-Ленца: - для постоянного, - для переменного тока.

Выделение количества теплоты, т.е. увеличение внутренней энергии кристаллической решетки проводника, происходит за счет энергии разогнанных электрическим полем свободных зарядов при их взаимодействии с ионами решетки.

Количество выделившейся теплоты з а время dt (в неподвижном металлическом проводнике) можно рассчитать как работу поля по перемещению заряда dq: . Закон Джоуля –Ленца – это проявление закона сохранения энергии при протекания тока в неподвижном проводнике в случае, когда работа поля переходит только в тепло.

САМОСТ.X закономерности: 1) последовательного соединения проводников; 2) параллельного соединения проводников.

§ 28 ЗАКОНЫ ОМА И ДЖОУЛЯ – ЛЕНЦА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ.

Поскольку направленное движение зарядов обеспечивается электрическим полем в проводнике, получим выражения экспериментальных законов, в которые входит характеристика электрического поля – напряженность.

Рассмотрим внутри однородного, изотропного проводника со стационарным током объем dV в виде тонкого прямого цилиндра длиной dl и сечением dS. Пусть образующие цилиндра параллельны линиям вектора напряженности и он настолько мал, что поле внутри можно считать однородным. , . Используя закон Ома и связь между плотностью и силой тока, получим: или - закон Ома в дифференциальном виде. Найдем количество теплоты, выделившееся в объеме dV при протекании тока в течение промежутка времени dt:

Введем удельную тепловую мощность тока, т.е. количество теплоты, выделяющееся при прохождении тока в единичном объеме за единицу времени:

Закон Джоуля-Ленца в дифференциальном виде: позволяет определить количество теплоты, выделяющееся в единицу времени в данном месте проводника, так как плотность тока и напряженность – характеристики точки проводника.

Законы Ома и Джоуля – Ленца в таком представлении не содержат дифференциалов (производных), а называются так потому, что устанавливают связь между локальными величинами, характеризующих точку внутри проводника.

В такой локальной форме эти законы могут быть применены к любым проводникам вне зависимости от их формы, однородности, а также природы причин, возбуждающих ток.

Не нашли, что искали? Воспользуйтесь поиском: