ЗАКОН АМПЕРА. СИЛА ЛОРЕНЦА.

Закон Био-Савара-Лапласа–Ампера экспериментально проверить нельзя, но следствия из него подтверждаются на практике.

Во всех точках пространства, окружающего произвольный ток, всегда существует обусловленное этим током поле сил, которое по сложившейся исторически терминологии называется магнитным полем.

По аналогии с электростатикой можно ввести силовую характеристику точки магнитного поля – вектор магнитной индукции:

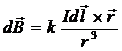- закон Био-Савара-Лапласа для расчета индукции магнитного поля, создаваемого элементом тока в некоторой точке (рис.70). Экспериментально проверить эту формулу нельзя, но можно рассчитать индукцию магнитного поля, созданного всем контуром с током, используя установленный на опыте принцип суперпозиции магнитных полей: 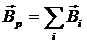. -лишь формальная запись, на практике интегрирование возможно лишь для проекций вектора магнитной индукции.

Единицы измерения Тл (Тесла).

Если задана объемная плотность тока,

то: . Тогда

Магнитное поле порождается движущимися зарядами (токами). Если скорость направленного движения зарядов в проводнике , то . Тогда:

Индукцию магнитного поля точечного заряда, движущегося с постоянной нерелятивистской скоростью (рис.71) можно определить по формуле:

В_земли~5*10^-5Тл, В_мозга~10^-11Тл.

В_max ~150 Тл - получена в виде импульса.

САМОСТОЯТ.XI: рассчитать индукцию магнитного поля: 1)бесконечного длинного прямого проводника с током I в точке на расстоянии b от него;

2)полубесконечного длинного прямого проводника с током I в точке на расстоянии b от него.

В законе Био-Савара-Лапласа-Ампера рассматривалось взаимодействие элементов токов двух контуров.

Выражение определяет индукцию магнитного поля, созданного элементом тока 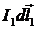в месте расположения элемента тока .

Используя принцип суперпозиции магнитных полей, можно найти индукцию магнитного поля, создаваемого всем первым контуром с током в месте расположения второго элемента тока. В этом случае на второй элемент тока будет действовать сила .

Сила, действующая на элемент тока в магнитном поле, называется силой Ампера, а формула, позволяющая рассчитать эту силу – закон Ампера:

Так как , то закон Ампера может быть записан в виде: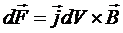

Интегрируя эти выражения по объемным или линейным элементам тока, можно найти силу, действующую на тот или иной объем проводника или его линейный участок.

Экспериментально показано, что магнитное поле также действует на движущиеся заряды. Сила, действующая на движущийся электрический заряд со стороны электромагнитного поля, называется силой Лоренца.

Получим формулу для магнитной составляющей силы Лоренца. Используем для этого формулу для силы Ампера, действующей на элемент тока в магнитном поле: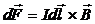

Если ток прекращается, то исчезает сила Ампера, но сила тока

, где q₀ - величина свободного заряда, а N – число свободных зарядов, проходящих через поперечное сечение проводника за dt.

Если средняя скорость направленного движения свободных зарядов 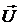, то

- сила, действующая со стороны магнитного поля на движущийся заряд.

Если заряд двигается в пространстве, в котором существуют одновременно электрическое и магнитное поле, то на него действует сила Лоренца:

Сила Лоренца является причиной появления силы Ампера.

САМОСТОЯТ. XII:

1)обосновать притяжение или отталкивание проводников с током;

2)получить формулу для силы взаимодействия на единицу длины, возникающей между двумя параллельными проводниками с токами I₁ и I₂;

3)обосновать введение 1 Ампера.

Не нашли, что искали? Воспользуйтесь поиском: