ТЕОРЕМА О ЦИРКУЛЯЦИИ ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ. ВИХРЕВОЙ ХАРАКТЕР МАГНИТНОГО ПОЛЯ.

Теорема о циркуляции вектора магнитной индукции поля постоянных токов в вакууме может быть доказана на основе закона Био-Савара, что, в общем случае, достаточно сложно.

- циркуляция вектора магнитной индукции по любому замкнутому контуру равна произведению магнитной постоянной на алгебраическую сумму токов охватываемых этим контуром.

Ток считается положительным, если его направление связано с направлением обхода по контуру правилом правого винта (рис.75).

РИС.75 РИС.76 РИС.77

Если ток распределен по объему, в котором расположен контур, то полный ток охваченный контуром , где интеграл берется по произвольной поверхности натянутой на контур, плотность тока соответствует точке расположения площадки . В этом случае теорема о циркуляции:

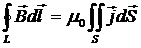
Покажем справедливость теоремы на примерах.

ПРИМЕР 1. Контур охватывает прямолинейный бесконечно длинный провод с током, причем контур расположен в плоскости перпендикулярной проводу (рис.76). Найдем циркуляцию вектора магнитного поля, используя формулу для расчета индукции поля, полученную методом суперпозиции 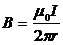. Скалярное произведение под интегралом можно представить (рис.77):

РИС.78 РИС.79

Если замкнутый контур L^` не охватывает ток (рис.78),

то и циркуляция также равна нулю.

ПРИМЕР 2. Контур лежит не в плоскости перпендикулярной проводу (рис.79). Разложим вектор на составляющие вектора, один из которых лежит в плоскости перпендикулярной проводу, а второй перпендикулярен этой плоскости:

Циркуляция вектора магнитной индукции определяется только «проекцией» контура на плоскость перпендикулярную проводу.

ПРИМЕР 3. Если контур охватывает несколько токов, то вектор индукции результирующего поля: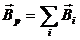

ПРИМЕР 4. Если ток непрерывно распределен в объеме, в котором расположен контур, то полный ток, охватываемый контуром , где интеграл берется по произвольной поверхности натянутой на контур.

Тогда:

РИС.80 РИС.81 РИС.82 РИС.83

Теорема о циркуляции позволяет достаточно просто рассчитать индукцию магнитного поля по известному распределению токов, если можно выбрать контур, вдоль которого модуль вектора магнитной индукции и направление постоянно.

В простейшем варианте можно выбрать контур, полностью совпадающий с линией магнитной индукции как в поле прямого тока (рис.80), тороида (рис.81).

Поле внутри соленоида (рис.82) тем более однородно, чем больше длина соленоида по сравнению с его диаметром. Для «бесконечного» соленоида снаружи вблизи его поверхности магнитного поля нет и можно выбрать контур, лишь часть которого совпадает с линией магнитной индукции (рис.83).

Ток, охватываемый контуром , где N – число витков с током, охваченных контуром. Тогда: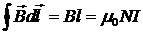

Следовательно, индукцию магнитного поля внутри «бесконечного» соленоида можно рассчитать по формуле

, где n – число витков соленоида на единицу длины.

Факт, что циркуляция вектора магнитной индукции по замкнутому контуру не равна нулю, означает, что, в отличие от электростатического, магнитное поле – не потенциально.

Используем теорему Стокса 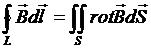и сравним это выражение с записью теоремы о циркуляции вектора магнитной индукции в случае непрерывного распределения тока в некотором объеме.

- дифференциальная (локальная) форма теоремы о циркуляции. Математическая констатация того факта, что линии вектора магнитной индукции замкнуты вокруг вектора плотности тока по правилу правого буравчика и поэтому магнитное поле называют вихревым или соленоидальным.

Используем, что или с помощью определителя:

, .

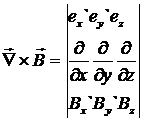Не нашли, что искали? Воспользуйтесь поиском: