Элементы квантовой механики. Формула де Бройля, выражающая связь длины волны l с импульсом движущейся частицы

Формула де Бройля, выражающая связь длины волны l с импульсом движущейся частицы

(46)

Соотношения неопределенностей

А)Для координаты и импульса частицы

, (47)

где D p_x – неопределенность проекции импульса частицы на ось x; D x – неопределенность ее координаты.

Б)Для энергии и времени

, (48)

где D Е – неопределенность энергии данного квантового состояния; D t – время пребывания системы в этом состоянии.

Одномерное временное уравнение Шредингера

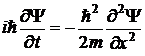(49)

Волновая функция, описывающая одномерное движение свободной частицы

(50)

эту функцию можно представить в виде:

(51)

где первый множитель

- координатная часть волновой функции

второй множитель

- временная часть волновой функции

Одномерное уравнение Шредингера для стационарных состояний

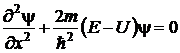(52)

где Е – полная энергия частицы; U=U(x) – потенциальная энергия частицы; y=y(x) – координатная (или амплитудная) часть волновой функции.

Вероятность обнаружить частицу в интервале от x до x+dx (в одномерном случае) выражается формулой

(53)

Вероятность обнаружить частицу в интервале от x ₁ до x ₂ находится интегрированием dW в указанных пределах:

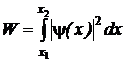(54)

Вероятность обнаружить частицу в интервале от -¥ до +¥

(55)

Эта формула называется условием нормировки. Она означает, что если частица существует то мы всегда сможем ее обнаружить где-нибудь на бесконечном интервале.

Собственное значение энергии Е_n частицы, находящейся на n-ом энергетическом уровне в бесконечно глубоком одномерном прямоугольном потенциальном ящике, определяется формулой

(n =1, 2, 3, …) (56)

где l – ширина потенциального ящика.

Соответствующая этой энергии собственная волновая функция имеет вид

(57)

Не нашли, что искали? Воспользуйтесь поиском: