Примеры решения задач. На стеклянную призму с преломляющим углом q = 50° падает луч света под углом a = 30°

Задача 1

На стеклянную призму с преломляющим углом q = 50° падает луч света под углом a = 30°. Определить угол отклонения s луча призмой, если показатель преломления n стекла равен 1,56.

Решение.

Принято решать задачи в общем виде, получая в результате итоговое выражение для искомой величины. Но данную задачу целесообразно решать, производя промежуточные вычисления. Точность расчётов несколько теряется, но зато решение становится более простым и наглядным.

Из рисунка видно, что: , (1) а углы g1 и g2 можно выразить через углы a, a¢, b, b¢, которые и нужно последовательно вычислить. Из закона преломления: можно выразить b: , b = 18,7°;

Из рисунка видно, что угол падения на вторую грань призмы e₂^/ равен:

b¢ =31,3°;

Угол b¢ меньше предельного (b¢_пред):

,

поэтому на второй грани луч преломится и выйдет из призмы.

Опять-таки по закону преломления:

,

откуда можно выразить e₁^/:

,

b¢ =54,1°.

Теперь можно найти углы g₁ и g₂:

,

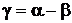g = 11,3°;

g¢ = 22,8°.

Остаётся по формуле (1) найти угол s:

Задача 2

На толстую стеклянную пластинку, покрытую очень тонкой плёнкой с показателем преломления 1,4, падает нормально параллельный пучок монохроматического света (l = 0,6 мкм). Отражённый свет максимально ослаблен вследствие интерференции. Определить толщину d плёнки.

Решение.

Из пучка, падающего на плёнку, выделим луч SA. Ход этого луча в общем случае, когда угол падения a ¹ 0, показан на рисунке.

В точках A и B падающий луч частично отражается и частично преломляется. Отражённые лучки AS ₁ и BCS ₂ падают на собирающую линзу L, пересекаются в её фокусе F и интерферируют между собой.

Так как показатель преломления воздуха (n ₁ = 1.00029) меньше показателя преломления вещества плёнки (n ₂ = 1.4), который, в свою очередь, меньше показателя преломления стекла (n ₃ = 1.5), то в обоих случаях отражение происходит от оптически более плотной среды. Поэтому фаза колебания луча AS ₁ при отражении в точке A изменяется на p; и точно так же на p изменяется фаза колебания луча BCS ₂ при отражении в точке B. Таким образом, результат интерференции этих лучей при пересечении в фокусе F линзы будет такой же, как если бы никакого изменения фазы у обоих лучей не было.

Условие максимального ослабления света при интерференции в тонких плёнках состоит в том, что оптическая разность хода D интерферирующих волн должна быть равна нечётному числу полуволн:

.

Как видно из рисунка, в данном случае оптическая разность хода:

.

Следовательно, условие минимума интенсивности примет вид:

.

Если угол падения a будет уменьшаться, стремясь к нулю, то:

,

,

где d – толщина плёнки.

В пределе при a = 0 получится:

,

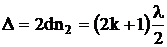откуда искомая толщина плёнки:

.

Полагая k = 0, 1, 2, 3, …, Получим ряд возможных значений толщины плёнки:

;

;

и так далее.

Задача 3

На диафрагму с круглым отверстием радиусом R = 1 мм падает нормально параллельный лучок света (длина волны l = 0,05 мкм). На пути лучей, прошедших через отверстие, помещают экран. Определить максимальное расстояние b_max от центра отверстия до экрана, при котором в центре дифракционной картины ещё будет наблюдаться тёмное пятно.

Решение.

Расстояние, при котором будет видно тёмное пятно, определяется числом зон Френеля, укладывающихся в отверстии. Если число зон чётное, то в центре дифракционной картины будет тёмное пятно.

Число зон Френеля, помещающихся в отверстии, убывает по мере удаления экрана от отверстия. Наименьшее чётное число равно двум. Следовательно, максимальное расстояние, при котором ещё будет наблюдаться тёмное пятно в центре картины, определяется условием, согласно которому в отверстии должны поместиться две зоны Френеля.

Как видно из рисунка, расстояние от точки наблюдения на экране до края отверстия больше, чем расстояние b = bmax, на величину 2(l/2). По теореме Пифагора: Если учесть, что l<< bmax и что членом l2 можно пренебречь, то последнее равенство можно переписать в виде:

,

откуда:

.

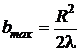Произведя вычисления, находим:

b_max = 1 м.

Задача 4

На дифракционную решётку нормально к её поверхности падает параллельный пучок света с длиной волны l = 0,5 мкм. Помещённая вблизи решётки линза проецирует дифракционную картину на плоский экран, удалённый от линзы на расстояние L = 1 м. Расстояние l между двумя максимумами интенсивности первого порядка, наблюдаемыми на экране, равно 20,2 см. Определить:

Постоянную d дифракционной решётки;

Число n штрихов на 1 см;

Число максимумов, которое даёт данная решётка;

Максимальный угол f_max отклонения лучей, соответствующих последнему дифракционному максимуму.

Решение.

Постоянная дифракционной решётки d, длина волны l и угол f отклонения лучей, соответствующих k -му дифракционному максимуму, связаны соотношением:

. (1)

В данном случае k = 1. Ввиду того, что l /2<< L:

, (2)

а из рисунка видно, что:

. (3)

С учётом равенств (2) и (3) соотношение (1) примет вид:

,

откуда постоянная решётки:

.

Подставляя данные, получим:

d = 4,95 мкм.

Число штрихов на 1 см находится из формулы:

,

n = 2,02×10³ см^-1.

Для определения числа максимумов, даваемых дифракционной решёткой, нужно найти максимальный порядок k_max исходя из того, что угол f отклонения лучей решёткой не может превышать 90°.

Из соотношения (1):

. (4)

k_max = 9,9.

Число k, однако, обязательно должно быть целым. Оно не может принять значение 10, так как в этом случае sin f должен был бы быть больше единицы, что невозможно. Значит, k_max = 9.

Таким образом, влево и вправо от центрального максимума будет наблюдаться по одинаковому числу максимумов, k_max = 9, то есть всего 18; необходимо учесть также центральный нулевой максимум, и тогда общее число максимумов N равно 19.

Для определения максимального угла отклонения лучей, соответствующих последнему дифракционному максимуму, нужно выразить из соотношения (4) синус сего угла:

.

Отсюда:

.

Подставив значения величин и произведя вычисления, получим:

f _max = 65,4°.

Задача 5.

Пластинка кварца толщиной d ₁ = 1 мм, вырезанная перпендикулярно оптической оси кристалла, поворачивает плоскость поляризации монохроматического света на угол f₁ = 20°. Определить:

Какова должна быть толщина d ₂ кварцевой пластинки, помещённой между двумя «параллельными» николями, чтобы свет был полностью погашен?

Какой длины l трубку с раствором сахара массовой концентрацией С = 0,4 кг/л надо поместить между николями для получения того же эффекта? Удельное вращение [a] раствора сахара равно 0,665 град/(м×кг×м^-3).

Решение.

Угол поворота плоскости поляризации кварцевой пластинкой определяется соотношением:

f = a d. (1)

Из сего соотношения можно выразить искомую толщину d₂ пластинки:

, (2)

где f₂ – угол поворота плоскости поляризации, при котором свет будет полностью погашен (f₂ = 90°).

Постоянную вращения для кварца также можно найти с помощью соотношения (1), подставив заданные в условии величины:

.

Подставив это выражение для a в формулу (2), получим:

;

d₂ = 4,5 мм.

Длину трубки с сахарным раствором можно найти из соотношения:

,

где d – толщина раствора сахара, равная в данном случае длине трубки l. Отсюда получим:

.

Подставив значения всех величин и произведя вычисления, найдём:

l = 0,38 м.

Задача 6.

Длина волны l _m, на которую приходится максимум энергии в спектре излучения чёрного тела, равна 0,58 мкм. Определить максимальную спектральную плотность энергетической светимости , рассчитанную на интервал длин волн Dl = 1 нм вблизи l _m.

Решение.

Максимальная спектральная плотность энергетической светимости пропорциональна пятой степени температуры:

. (1)

Температуру Т можно выразить из закона смещения Вина l _m = b / Т, откуда:

. (2)

Подставив полученное выражение (2) в формулу (1), найдём:

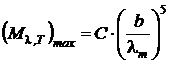. (3)

Значение С в таблицах даётся в единицах СИ, в которых единичный интервал длин волн Dl = 1 м. По условию же задачи требуется вычислить спектральную плотность энергетической светимости, рассчитанную на интервал длин волн 1 нм. Значение С нужно таким образом пересчитать на заданный интервал:

С = 1,30×10^-5 Вт/(м³×К⁵) = 1,30×10^-5 Вт/(м²×м×К⁵) = 1,30×10^-14 Вт/(м²×нм×К⁵).

Вычисление по формуле (3) даёт:

Задача 7

Фотон с энергией e = 0,75 МэВ рассеялся на свободном Электроне под углом q = 60°. Принимая, что кинетическая энергия и импульс электрона до соударения с фотоном были пренебрежимо малы, определить:

Энергию e^/ рассеянного фотона;

Кинетическую энергию Т электрона отдачи;

Направление его движения.

Решение.

1. Энергию рассеянного фотона можно найти, воспользовавшись формулой Комптона:

.

Выразив длины волн l и l¢ через энергии e и e¢ соответствующих фотонов, получим:

.

Разделим обе части последнего равенства на hc:

.

Обозначив энергию покоя электрона m ₀ c ² через Е ₀, выразим e¢:

. (1)

Подставив числовые значения величин, получим:

e¢ = 0,43 МэВ.

2. Кинетическая энергия электрона отдачи, как это следует из закона сохранения энергии, равна разности между энергией e падающего фотона и энергией e¢ рассеянного фотона:

Т = e - e¢ = 0,32 МэВ.

3. Направление движения электрона отдачи можно найти, применив закон сохранения импульса, согласно которому импульс падающего фотона равен векторной импульсов рассеянного фотона и электрона отдачи :

.

Векторная диаграмма импульсов изображена на рисунке. Все векторы проведены из точки О, где находится электрон в момент соударения с фотоном. Угол f определяет направление движения электрона отдачи. Из треугольника ОСD находим: , или: .

Так как и , то:

. (2)

Формулу (2) надо преобразовать так, чтобы угол f выражался непосредственно через величины e и q, заданные в условии задачи. Из формулы (1) следует:

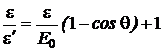. (3)

Заменим в формуле (2) соотношение e/e¢ по формуле (3):

.

Применив формулы тригонометрии:

,

;

после соответствующих преобразований получим:

. (4)

После вычисления по формуле (4) получим tg f = 0,701, откуда f = 35°.

Задача 8.

Вычислить радиус первой орбиты атома водорода (боровский радиус) и скорость электрона на этой орбите.

Решение.

Согласно теории Бора, радиус r орбиты и скорость V электрона на этой орбите связаны равенством:

.

Так как в задаче требуется определить величины, относящиеся к первой орбите, то главное квантовое число n = 1 и данное выше равенство принимает вид:

. (1)

Для определения двух неизвестных величин r и V необходимо ещё одно уравнение, в качестве которого можно взять уравнение движения электрона. Согласно теории Бора, электрон вращается вокруг ядра. При этом сила взаимодействия между электрическими зарядами ядра и электрона сообщает электрону центростремительное ускорение. На основании второго закона Ньютона можно записать:

,

где e и m – заряд и масса электрона, или:

. (2)

Совместное решение равенств (1) и (2) относительно r даёт:

.

Подставив в это выражение числовые значения, получим:

r = 5,29×10-11 м.

Из равенства (1) получим выражение скорости электрона на первой орбите:

.

Произведя по этой формуле вычисления, найдём:

V = 2,18×10⁶ м/с.

Задача 9.

Определить начальную активность А ₀ радиоактивного магния ²⁷Mg массой m = 0,2 мкг, а так же радиоактивность А по истечении времени t = 1 ч. Предполагается, что все атомы изотопа радиоактивны.

Решение.

Начальная радиоактивность изотопа:

, (1)

где l - постоянная радиоактивного распада, а N ₀ – количество атомов изотопа в начальный момент (t = 0).

Если учесть, что:

;

;

то формула (1) примет вид:

. (2)

Выразим входящие в эту формулу величины в СИ и произведём вычисления:

А ₀ = 5,15×10¹² Бк.

Активность изотопа уменьшается со временем по закону:

. (3)

Заменив в формуле (3) постоянную распада l её выражением, получим:

.

Так как eln2 = 2, то окончательно:

.

Сделав подстановку числовых значений, получим:

А = 8,05×10¹⁰ Бк.

Задача 10.

Вычислить дефект массы Dm и энергию связи Е_св ядра ¹¹₅В.

Решение.

Дефект массы ядра определяется по формуле:

. (1)

Вычисление дефекта массы выполним во внесистемных единицах (а.е.м.). Для ядра ¹¹₅В:

Z = 5, А = 11. Массы нейтральных атомов водорода и бора, а так же нейтрона (n) найдём из соответствующей таблицы.

Подставим найденные массы в выражение (1) и произведём вычисления:

D m = 0,08186 а.е.м.

Энергия связи ядра определяется соотношением:

. (2)

Энергию связи также найдём во внесистемных единицах (МэВ). Для этого дефект массы подставим в выражение (2) в а.е.м., а коэффициент пропорциональности (с²) – в МэВ/(а.е.м.), то есть:

Е_св = 931,4×0,08186 МэВ = 76,24 МэВ.

Задача 11.

Кинетическая энергия электрона Т в атоме водорода составляет величину порядка 10 эВ. Используя соотношение неопределённостей, оценить минимальные линейные размеры атома.

Решение.

Неопределённость координаты и импульса электрона связаны соотношением:

. (1)

Из этого соотношения следует, что чем точнее определяется положение частицы в пространстве, тем более неопределённым становится импульс, а значит, и энергия частицы. Пусть атом имеет линейные размеры l, тогда электрон атома будет находиться где-то в пределах области с неопределённостью D x = l/2. Соотношение неопределённостей (1) можно записать в этом случае в виде (l/2)D p ³ h, откуда:

. (2)

Физически разумная неопределённость импульса D p, во всяком случае, не должна превышать значения самого импульса, то есть p ³ D p. Импульс связан с кинетической энергией Т соотношением:

.

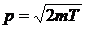Заменим D p значением 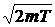- такая замена не увеличит l. Переходя от неравенства (2) к равенству, получим:

.

Подставив числовые значения и произведя вычисления, получим:

l_min = 124 пм.

Задача 12.

Электрон с энергией Е = 4,9 эВ движется в положительном направлении оси х. Высота U ₀ потенциального барьера равна 5 эВ. При какой Ширине d барьера вероятность W прохождения электрона через него будет равна 0,2?

Решение.

Вероятность W прохождения частицы через потенциальный барьер по своему физическому смыслу совпадает с коэффициентом прозрачности D (W = D). Тогда вероятность того, что электрон пройдёт через прямоугольную потенциальную ступень, выразится соотношением: , (1) где m – масса электрона. Потенцируя это выражение, получим:

.

Для удобства вычислений изменим знак у правой и левой частей сего равенства и выразим d:

.

Входящие в эту формулу величины выразить в единицах СИ и произведём вычисления:

d = 4,95×10^{-10 м = 0,495 нм.}

Учитывая, что формула (1) приближённая и вычисления носят оценочный характер, можно принять d @ 0,5 нм.

Не нашли, что искали? Воспользуйтесь поиском: