Циркуляция вектора индукции магнитного поля.

Закон полного тока

Интеграл называется циркуляцией вектора индукции магнитного поля по замкнутому контуру.

Для определения магнитной индукции с симметричным расположением витков с током вычисляется интеграл по замкнутому контуру вектора индукции магнитного поля .

Например, для контура в виде окружности радиусом циркуляция вектора индукции магнитного поля прямолинейного проводника с током I равна

.

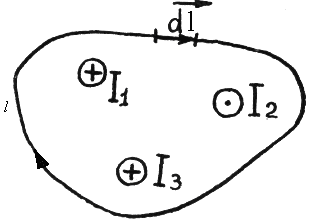Пусть произвольный контур l охватывает проводников с токами различного направления. В этом случае, ,

,

где - проекция вектора индукции магнитного поля от -го проводника с током на участке контура , - алгебраическая сумма токов, охватываемых контуром l.

Ток считается положительным, если направление линий индукции его магнитного поля совпадает с направлением обхода контура и отрицательным, если не совпадает. В нашем случае .

Закон полного тока:

Если контур l охватывает N проводников с одинаковым током I, тогда

Не нашли, что искали? Воспользуйтесь поиском: