
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Индуктивность. Самоиндукции
Если в пространстве, где находится проводящий контур с током I, нет ферромагнетиков, то вектор магнитной индукции  (см. закон Био-Савара - Лапласа, а значит и поток вектора магнитной индукции Ф через контур пропорционален силе тока Ф~I,и можно ввести коэффициент пропорциональности
(см. закон Био-Савара - Лапласа, а значит и поток вектора магнитной индукции Ф через контур пропорционален силе тока Ф~I,и можно ввести коэффициент пропорциональности
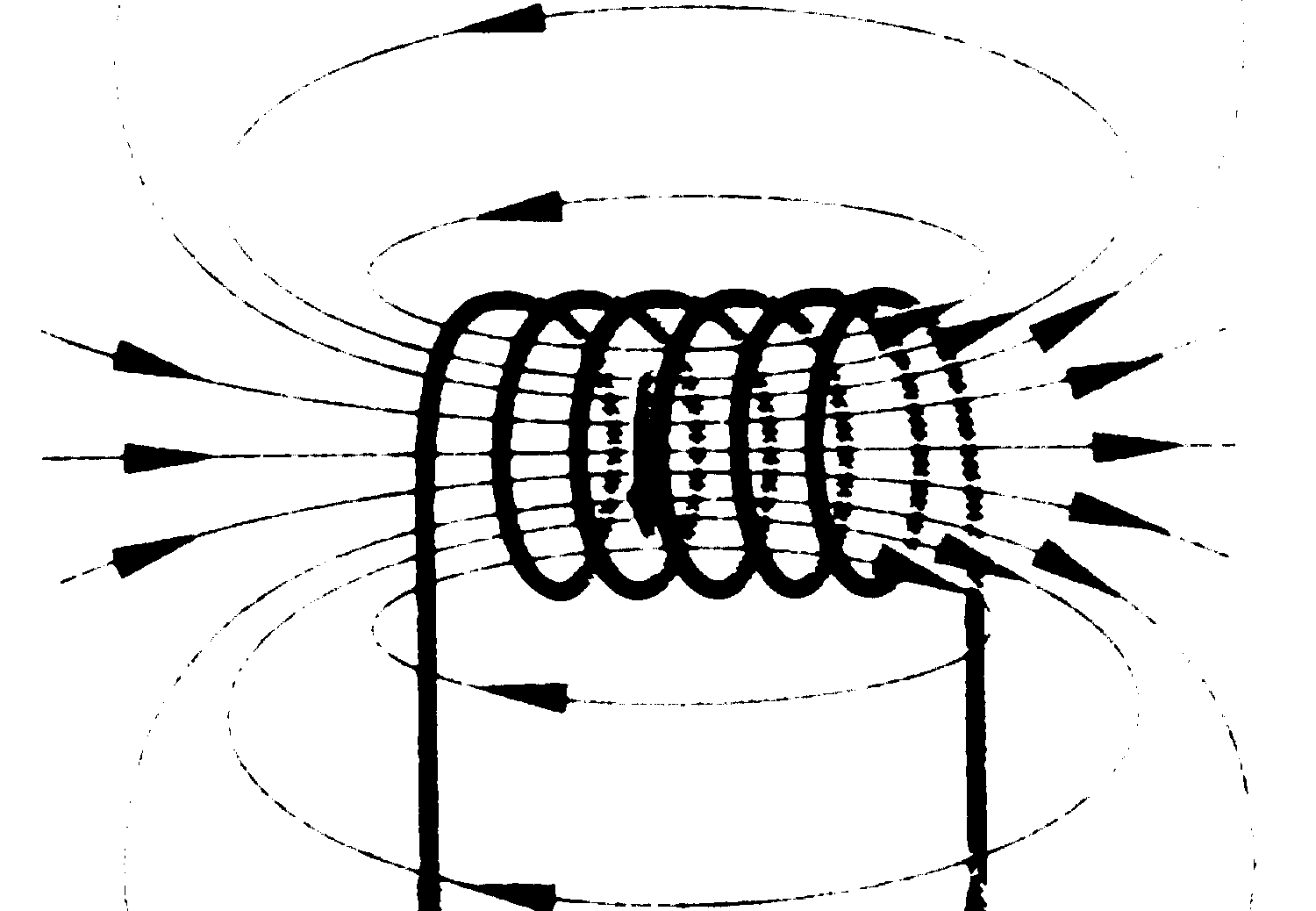
|

|
| S |
| N витков |
| l |
Здесь L - индуктивность контура. Индуктивность всегда положительна и зависит только от формы и размеров контура, а также от магнитных свойств окружающей среды. Единица измерения индуктивности- генри (Гн). [Гн] = [Вб]/[А].
Индуктивность длинного соленоида объемом V=Sl,

|
 , магнитной проницаемостью вещества внутри соленоида -
, магнитной проницаемостью вещества внутри соленоида -  . Здесь S - площадь поверхности одного витка, l - длина соленоида и N- общее число витков. Магнитное поле в длинном соленоиде однородно и модуль его вектора магнитной индукции
. Здесь S - площадь поверхности одного витка, l - длина соленоида и N- общее число витков. Магнитное поле в длинном соленоиде однородно и модуль его вектора магнитной индукции  .
.
Выбирая вектор нормали параллельным вектору магнитной индукции для магнитного потока через один виток соленоида, получаем Ф = BS  .
.
Магнитный поток Ψ, пронизывающий N одинаковых витков, (потокосцепление) определяется соотношением
Ψ = NФ =  .
.
Тогда, индуктивность соленоида равна  .
.
При изменении силы тока в произвольном контуре меняется вектор магнитной индукции, а значит и магнитный поток через этот контур. Следовательно, в нем самом должна наводится эдс, которая называется эдс самоиндукции εs. Явление возникновения индукционного электрического тока в замкнутом проводящем контуре при изменении тока в нем называется самоиндукцией. Так как Ф = LI, то
εS  .
.
Если при изменении тока в контуре его индуктивность не меняется (т.е. не меняется конфигурация контура и нет ферромагнитной среды), то
εS  .
.
Используя закон Ома, получим выражение для тока самоиндукции
 .
.
Знак минус показывает, что эдс «вызывает» индукционный ток, направленный против изменения первоначального тока, т.е. в соответствии с правилом Ленца. Эдс самоиндукции противодействует первоначальному току, когда он увеличивается и поддерживает его, когда он уменьшается.
Определим на примере одного витка с током направление индукционного тока исходя из выражения для тока самоиндукции.
Выберем за положительное направление обхода контура направление протекания первоначального тока I в нем (белая стрелка вниз) т.е. I > 0. Тогда вектор нормали  направлен слева - направо (рис.). Вектор магнитной индукции
направлен слева - направо (рис.). Вектор магнитной индукции  такого витка с током также направлен в эту
такого витка с током также направлен в эту

|

|

|

|

|

|

|

|

|

|

|

|

|
| а |
| б |
сторону (белая стрелка вправо) и, следовательно, так как  и
и  сонаправлены, магнитный поток первоначального тока через плоскость, ограниченную контуром, положителен.
сонаправлены, магнитный поток первоначального тока через плоскость, ограниченную контуром, положителен.
Пусть первоначальный ток возрастает, т.е.  > 0 (рис.а). Тогда ток самоиндукции
> 0 (рис.а). Тогда ток самоиндукции  < 0 (черная стрелка вверх). Таким образом, в соответствии с правилом Ленца индукционный ток отрицателен. Это значит, что он направлен в сторону, обратную направлению первоначального тока, и мешает первоначальному току возрастать. При таком направлении тока самоиндукции его вектор магнитной индукции
< 0 (черная стрелка вверх). Таким образом, в соответствии с правилом Ленца индукционный ток отрицателен. Это значит, что он направлен в сторону, обратную направлению первоначального тока, и мешает первоначальному току возрастать. При таком направлении тока самоиндукции его вектор магнитной индукции  составляет угол
составляет угол  с вектором нормали к контуру, а магнитный поток через плоскость ограниченную контуром - отрицателен. Пусть первоначальный ток уменьшается, т.е.
с вектором нормали к контуру, а магнитный поток через плоскость ограниченную контуром - отрицателен. Пусть первоначальный ток уменьшается, т.е.  < 0 (рис. б). Тогда ток самоиндукции
< 0 (рис. б). Тогда ток самоиндукции  > 0 (черная стрелка вниз). Таким образом, в соответствии с правилом Ленца индукционный ток положителен. Это означает, что он направлен по направлению первоначального тока и мешает первоначальному току уменьшаться, т.е. поддерживает его. При таком направлении тока самоиндукции его вектор магнитной индукции
> 0 (черная стрелка вниз). Таким образом, в соответствии с правилом Ленца индукционный ток положителен. Это означает, что он направлен по направлению первоначального тока и мешает первоначальному току уменьшаться, т.е. поддерживает его. При таком направлении тока самоиндукции его вектор магнитной индукции  параллелен вектору нормали к контуру, а магнитный поток через плоскость ограниченную контуром - положителен.
параллелен вектору нормали к контуру, а магнитный поток через плоскость ограниченную контуром - положителен.
. Переходные процессы при размыкании и замыкании цепи
Характерные проявления явления самоиндукции наблюдаются при размыкании и замыкании тока в электрической цепи.
1) Исчезновение тока при размыкании цепи
| б |
| I0 |
| t |
| τ |
| I0/ e |
| А |
| L |
| I |
| R |
| ε |
| K |
| I |
| R |


| а |
Пусть цепь состоит из источника тока с эдс  и нулевым внутренним сопротивлением, резистора с сопротивлением R, катушки индуктивности с постоянной индуктивностью L и ключа K. Первоначально ключ находится в нижнем положении (рис. а), и в цепи течет ток
и нулевым внутренним сопротивлением, резистора с сопротивлением R, катушки индуктивности с постоянной индуктивностью L и ключа K. Первоначально ключ находится в нижнем положении (рис. а), и в цепи течет ток  .
.
В момент t = 0 повернем ключ по направлению движения часовой стрелки из нижнего положения в верхнее и отключим цепь от источника. Ток через индуктивность начнет убывать. Это приведет к возникновению эдс самоиндукции εS  , которая противодействует, по правилу Ленца, убыванию тока. Так как это единственное эдс, которое действует в цепи, то в каждый момент времени ток в контуре - это ток самоиндукции
, которая противодействует, по правилу Ленца, убыванию тока. Так как это единственное эдс, которое действует в цепи, то в каждый момент времени ток в контуре - это ток самоиндукции
 или RI =
или RI =  .
.
Преобразуем это выражение к виду  .
.
За время от 0 до t ток изменится от I0 до I. Проинтегрируем правую и левую часть в указанных пределах.
 .
.
Взяв интегралы, получим
 или
или  .
.
Так как разность логарифмов равна логарифму отношения, то  . Потенцируя это уравнение, получаем
. Потенцируя это уравнение, получаем  Или I(t) = I0e
Или I(t) = I0e  , где
, где  - время релаксации, т.е. время, в течение которого, считая от момента размыкания цепи, сила тока уменьшается в
- время релаксации, т.е. время, в течение которого, считая от момента размыкания цепи, сила тока уменьшается в  раз. Зависимость представлена на рис. б.
раз. Зависимость представлена на рис. б.
2) Появление тока при замыкании цепи
| I |
| R |
| L |
| ε |
| t |
| А |
| K |
| I0 |
| I |
| R |


| а |
| б |
Согласно закону Ома для замкнутой неоднородной цепи с несколькими источниками эдс IR = ε + εS= ε  .
.
Преобразуем это выражение к виду R(I  )
)  или
или  .
.
Введем постоянные величины под знак дифференциала
 .
.
За время от 0 до t ток изменяется от 0 до I, а выражение, стоящее под дифференциалом, - от  до
до  . Проинтегрируем правую и левую часть в указанных пределах.
. Проинтегрируем правую и левую часть в указанных пределах.  . Тогда:
. Тогда:
 . Потенцируя, получаем:
. Потенцируя, получаем: 
 . Пусть
. Пусть  и
и  . Тогда выражение зависимости тока от времени принимает (рис. б) вид
. Тогда выражение зависимости тока от времени принимает (рис. б) вид  или
или
 .
.
Очевидно, что  - максимальный ток, установившийся в цепи при
- максимальный ток, установившийся в цепи при  , а
, а  - время установления тока, т.е. время, считая от момента замыкания, в течение которого сила тока достигает значения в (e-1)/e раз меньше максимально.
- время установления тока, т.е. время, считая от момента замыкания, в течение которого сила тока достигает значения в (e-1)/e раз меньше максимально.
Взаимная индукция
Явление возникновения индукционного тока в одном замкнутом проводящем контуре при изменении тока в другом называется взаимоиндукцией.
Рассмотрим два неподвижных контура с сопротивлениями R1 и R2, расположенные достаточно близко друг от друга. Если в первом контуре течет ток I1, то магнитное поле  этого тока создает магнитный поток Ф21 через поверхность второго контура, пропорциональный, как следует из закона Био-Савара-Лапласа, току I1 т.е. Ф21= L21I1.
этого тока создает магнитный поток Ф21 через поверхность второго контура, пропорциональный, как следует из закона Био-Савара-Лапласа, току I1 т.е. Ф21= L21I1.
Если магнитный поток зависит от времени, то во втором контуре возникает эдс индукции ε2i
ε2i= 
и течет индукционный ток
 .
.
Если во втором контуре течет ток I2, то магнитное поле  этого тока создает магнитный поток Ф12 через поверхность первого контура, пропорциональный токy I2, т.е. Ф12 = L12I2.
этого тока создает магнитный поток Ф12 через поверхность первого контура, пропорциональный токy I2, т.е. Ф12 = L12I2.
Если магнитный поток зависит от времени, то в первом контуре возникает эдс индукции ε12
ε12 = 
и течет индукционный ток
 .
.
Если L21 и L12 не зависят от времени, то
ε21 =  ,
,  ,
,
ε12 =  ,
,  .
.
Введенные коэффициенты пропорциональности L21 и L12 называются взаимными индуктивностями контуров. Взаимная индуктивность численно равна магнитному потоку сквозь один из контуров, создаваемому единичным током в другом контуре. Взаимные индуктивностизависят только от взаимной конфигурации контуров и магнитной проницаемости среды. Размерность коэффициентов - генри (Гн).
В отличие от индуктивности  коэффициенты взаимоиндукции могут быть как положительными, так и отрицательными. Несложно показать, что справедлива теорема взаимности: в отсутствии ферромагнитной среды взаимные индуктивности контуров
коэффициенты взаимоиндукции могут быть как положительными, так и отрицательными. Несложно показать, что справедлива теорема взаимности: в отсутствии ферромагнитной среды взаимные индуктивности контуров
L12 = L21.
Смысл этой теоремы состоит в том, что при пропускании одного и того же по величине тока  через любой из двух контуров магнитный поток через другой контур всегда будет одним и тем же, т.е Ф21= L21I = L12I = Ф 12. (на явлении взаимной индукции основано действие трансформаторов).
через любой из двух контуров магнитный поток через другой контур всегда будет одним и тем же, т.е Ф21= L21I = L12I = Ф 12. (на явлении взаимной индукции основано действие трансформаторов).
Не нашли, что искали? Воспользуйтесь поиском: