IV.1. Уравнение политропы. Определение показателя политропы.

Из физики известно четыре простейших процесса (изопроцесса):

1) изобарный;

2) изохорный;

3) адиабатный;

4) изотермический,

Для сравнения изобразим на рис.10 эти процессы, проходящими через общую точку А:

р 2

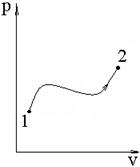
Но в целом ряде случаев реальные процессы, например рис.11, не соответствуют ни одному из изопроцессов.

Для выполнения теплотехнических расчётов в таких случаях, пусть даже с какими-то погрешностями, реальный процесс заменяется гипотетическим, имеющим формулу, удобную с точки зрения математических преобразований. Этому требованию удовлетворяет уравнение вида 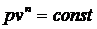. Так как это уравнение должно описывать всё многообразие реальных процессов, то в этом уравнении должен присутствовать коэффициент согласования (идентификации). Этим коэффициентом является показатель степени n, называемый показателем политропы. Так как n - коэффициент согласования, то, в отличие от показателя адиабаты k в уравнении Пуассона 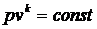, где k>1, показатель политропы может иметь любые значения в интервале (-¥,+¥). Показатель политропы определяется только путем обработки опытных данных.

Алгоритм определения показателя политропы n.

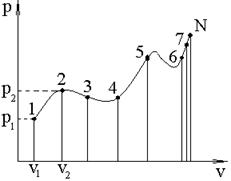
1) Разбиваем pv-диаграмму реального процесса на N точек (чем больше точек, тем точнее n).

2) Снимаем с pv-диаграммы реального процесса значение давления p_i удельного объёма v_i в каждой i-той точке и заносим в таблицу.

3) Для каждой i-той точки вычисляем значения ln p_i и ln v_i и заносим в таблицу.

4) Перестраиваем pv-диаграмму в координатах: ln p - ln v.

5) Аппроксимируем точки на графике в логарифмических координатах одной прямой, используя метод наименьших квадратов или другой аналогичный метод. Если это удаётся без значительных погрешностей, то тангенс угла наклона прямой к оси ln v равен показателю политропы.

На рис. 12 и 13 представлен пример определения показателя политропы.

i – номер точки	pi, Па	vi,	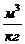ln p	ln v
	p1	v1	ln p 1	ln v 1
	p2	v2	ln p 2	ln v 2
…	…	…	…	…
N	pN	vN	ln p N	ln v N

Если все точки не укладываются удовлетворительно на одной прямой, то используется метод линейно-кусочной аппроксимации, по которому показатели политропы определяются для отдельных участков процесса.

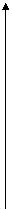ln p

.3. N

. 9

. 4

. 2

. 8

.1. 5

. 6. 7

В этом случае реальный процесс рассчитывается по уравнению pvⁿ = const при последовательно изменяющемся значении показателя политропы n: n₁, n₂, n₃ и т.д. Значения А,Q,U, найденные на отдельных участках процессов затем суммируются.

В тех случаях, когда расчёты выполняются для небольшого участка процесса или для всего процесса известны только две точки, можно использовать метод определения показателя политропы n по двум точкам.

1

Р₁

Р₂

V₁ V₂ V, м³/кг

Если реальный процесс задан pv-координатах, то используется уравнение политропы в виде

pvⁿ = p₁v₁ⁿ = p₂v₂ⁿ =const

После логарифмирования и приведения подобных, получим искомое значение n:

ln p₁ + n ln v₁ = ln p₂ + n ln v₂

ln p₁ – ln p₂ = n (ln v₂ - ln v₁)

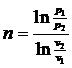(139)

В политропном процессе газ считается идеальным. Так как основное уравнение политропы pvⁿ =const по форме совпадает с уравнением адиабаты идеального газа pv^k =const (уравнение Пуассона), то без вывода запишем еще два уравнения политропы:

(140)

(141)

Для определения показателя политропы может использоваться любое из трех уравнений политропы.

Так как теплоёмкость является функцией процесса, то получим формулу для теплоёмкости в политропном процессе с_n:

Из общей формулы теплоёмкостей однородных систем (74) для политропного процесса имеем:

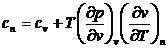(формула(76))

Так как в политропном процессе газ считается идеальным, то

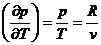(формула(77))

Требуется найти 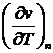. Для этого воспользуемся уравнением политропы (140):

.

Логарифмируя и дифференцируя это уравнение, приводя подобные получим:

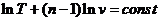
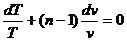
Откуда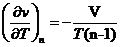

Подставим найденное значение в уравнение (76):

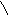
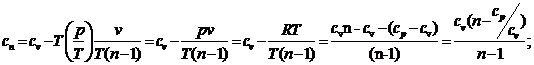
Окончательно

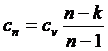(142)

В (142) показатель адиабаты k>1, в то время как nÎ(-¥, +¥).

При 1<n<k значение c_n получается отрицательным. С физической точки зрения это трудно объяснимо, поэтому, придавая отрицательной величине c_n формальный характер, вычисление А, Q, U проводим с этим отрицательным значением.

Изопроцессы, в силу универсальности уравнения 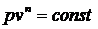, можно рассмотривать как частные случаи политропного процесса:

1) при n = 0 получается уравнение изобарного процесса (p=const);

2) при n = 1 – уравнение изотермического процесса (pv=const);

3) при n = k – уравнение адиабатного процесса pv^k=const (или S=const);

4) 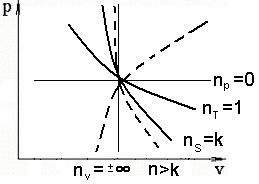при n = ±¥ - уравнение изохорного процесса (v=const).

Не нашли, что искали? Воспользуйтесь поиском: