III.1. Три группы формул для вычисления энтропии.

Энтропию называют «тенью» внутренней энергии и она, также как U, является функцией состояния. Таким образом, dS – полный дифференциал энтропии.

Энтропию, как функцию состояния, для термодеформационной системы можно выразить через любое из трех сочетаний термодинамических параметров T, V, P: S=S(T, V), S=S(T,P) и S=S(P,V) и получить три группы равнозначных формул.

· Получим первую группу формул для расчета энтропии.

Пусть S = S(T,V),

Как было получено ранее (88)

тогда

Здесь - третий тип дифференциальных соотношений термодинамики

, тогда окончательно

(104)

Формула (104) применима как для реальных, так и для и идеальных газов.

Для идеального газа эта формула имеет более простой вид. Получим эту формулу. Для идеального газа известно (77):

Подставим (77) в (104) и окончательно получим:

(105)

Формула (105) применима только для идеального газа.

Найдем неопределенный интеграл S из (105)

.

Полагаем

Здесь - средняя массовая изохорная теплоёмкость

или

(106)

Здесь,

где - показатель адиабаты.

Попутно рассмотрим адиабатный обратимый процесс, то есть процесс при S=const

Так как в (106) S₀ и константы, то для выполнения условия S=const должно выполняться условие

Это уравнение называется уравнением адиабаты идеального газа или уравнением Пуассона.

Для практики наибольший интерес представляет не абсолютное значение S, а её изменение dS.

Найдем определенный интеграл энтропии по формуле (105):

Пусть тогда

(107)

Из (107) можно получить два частных случая:

(108)

(109)

Здесь S имеет размерность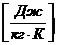

Энтропия – это мера неупорядоченности системы (чем больше энтропия, тем больше беспорядок).

При S = 0 должно отсутствовать не только макроскопическое, но и микроскопическое движение частиц, поэтому энтропия может быть равна нулю только при абсолютном нуле температур.

Но по 3-ему закону термодинамики (следствию тепловой теоремы Нернста) при T®0, S®0 абсолютный нуль температур недостижим.

В инженерной практике, начало отсчета энтропии может быть выбрано произвольно. Условились, за начало отсчёта энтропии принимать нормальные физические условия (н.ф.у.): p_н=101325 Па, T_н=273.15 K. Таким образом, при н.ф.у S=0.

При этом уравнение (107) примет вид

Индекс 2 опускаем, тогда окончательно энтропию можно вычислить по следующей формуле

(110)

Здесь v_н – удельный объём при нормальных физических условиях.

Из p_нv_н=RT_н,

Здесь µ - молекулярная масса газа.

Как известно, по закону Авогадро 1 Кмоль любого газа при одинаковых условиях занимает один и тот же объём, в частности при нормальных физических условиях 1 Кмоль любого газа занимает объём, равный 22,4 м³.

Во всех вышеприведённых формулах массовая изохорная теплоёмкость c_v бралась средним значением .

Получим формулы для случая линейной зависимости теплоёмкости от температуры c_v=c_0v+aT

Подставим это в (105)

Окончательно

(111)

Из (111) следуют два частных случая (Т=const и V=const)

(формула (108))

(112)

Принимая S=0 при нормальных физических условиях, получим формулы для расчёта энтропии:

(113)

· Получим вторую группу формул для расчёта энтропии.

Пусть S=S(T,P)

(114)

Формула (114) справедлива для любого газа и любого процесса

В качестве частного случая рассмотрим идеальный газ:

Для идеального газа из (78)

Подставим (78) в (114)

(115)

Найдем неопределенный интеграл S по формуле (115)

(116)

где S₀ – константа интегрирования

Пусть _, тогда

,

Выразим отношение 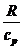через теплоемкости

Тогда

(117)

Попутно рассмотрим адиабатный процесс, полагая его обратимым. Тогда уравнение адиабатного процесса запишется в виде S=const

Так как в уравнение (117) при условии S=const правая часть также должна быть константой, то при с_р=const и S₀=const должно выполняться условие

(118)

Уравнение (118) называется уравнением адиабаты идеального газа или уравнением Пуассона.

Вернемся к (115) и найдем определенный интеграл энтропии:

(119)

Эта формула применима для любого процесса идеального газа.

Из (119) следуют два частных случая:

(120)

(121)

Если взять за начало отсчёта S нормальные физические условия, то из (119) получим зависимость для расчета энтропии:

(122)

Получим формулы второй группы для случая, когда изобарная теплоемкость линейно-зависит от температуры (с_р=с_0р+аТ). Подставим с_р в (115) и найдем определенный интеграл:

(123)

Эта формула применима для любого процесса идеального газа.

Из (123) следует два частных случая:

(формула (120))

(124)

Полагая за начало отчета S н.ф.у получим формулу для расчета энтропии идеального газа в любом процессе

(125)

· Получим третью группу формул:

Пусть S = S(p,v),

Здесь частные производные заменены произведением частных производных.

(126)

Формула (126) справедлива для всех процессов как реального так и для идеального газов.

В качестве частного случая рассмотрим идеальный газ:

Как известно, для идеального газа

,

,

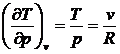Подставим эти значения частных производных в (126) и получим формулу, справедливую для всех процессов идеального газа:

(127)

Попутно рассмотрим обратимый адиабатный процесс (S=const) и найдем определенный интеграл (127):

.

Полагаем и

Тогда

В адиабатном процессе S=const и правая часть этого уравнения также является константой, если

(128)

Уравнение (128) называется уравнением адиабаты идеального газа или уравнением Пуассона.

Окончательно, адиабатные процессы идеального газа описываются тремя равнозначными уравнениями Пуассона.

;

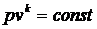; (129)

.

Вернемся к формуле (115) и возьмём определённый интеграл энтропии:

(130)

Из (130) следуют два частных случая:

(формула (121))

(формула (109))

Принимая за начало отсчёта S нормальные физические условия, из (130) получим формулу:

(131)

где - удельный объем идеального газа при н.ф.у.

Получим формулы для случая линейной зависимости теплоёмкостей от температуры:

c_v=c_0v+aT и c_p=c_0p+aT, где c_0v, c_0p, а – постоянные величины.

(132)

Найдём значение из уравнения Менделеева-Клапейрона после его логарифмирования и дифференцирования:

Подставим это выражение в (132)

(133)

Интегрируя (133) получим:

(134)

Из (134) следует три частных случая:

(135)

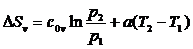(136)

Преобразуем эту формулу:

или

(формула (120))

Полагая S=0 при нормальных физических условиях, из (134) получим формулу для расчета значения энтропии идеального газа в любом процессе

(137)

Не нашли, что искали? Воспользуйтесь поиском: