Теплопроводность при нестационарном температурном поле

Решить задачу теплопроводности при нестационарном температурном поле – значить установить зависимость между температурой t, временем и координатами тела x,y,z. Такая зависимость получается решением дифференциального уравнения теплопроводности при определенных условиях однозначности.

При отсутствии внутренних источников тепла дифференциальное уравнение теплопроводности имеет вид

. (54)

Уравнение (54) является линейным, однородным дифференциальным уравнением второго порядка в частных производных. Решения такого уравнения обладают свойством наложения аналогично решениям обыкновенного однородного дифференциального уравнения: если t₁ и t₂ — частные решения уравнения, то выражение является также его решением при произвольных значениях постоянных С₁ и С₂. Поскольку у постоянных С₁, и С₂ возможны различные значения, уравнение типа (54) может иметь бесконечно большое количество частных решений.

Для решения уравнения теплопроводности, удовлетворяющего заданным условиям однозначности, берут сумму частных решений, в которых постоянные С_i имеют определенные значения. Соответствующим подбором постоянных C_i, удовлетворяют решение исходному дифференциальному уравнению и условиям однозначности.

К классическим методам решения уравнения теплопроводности относятся метод разделения переменных и метод источников.

Метод разделения переменных. По этому методу решается уравнение теплопроводности, а затем, исходя из начальных и граничных условий, определяются постоянные в общем решении. Частное решение t выражается произведением двух функций, одна из которых U(τ) зависит только от времени τ, а другая P(x,y,z) зависит только от координат

, (55)

где С – произвольная постоянная.

Подставляя решение (55) в уравнение (54) получим

. (56)

Уравнение (56) можно переписать так

. (57)

Левая часть уравнения(57) может зависеть только от или быть постоянным числом; она не зависит от координат. Правая часть может зависеть от координат или быть постоянным числом; она не зависит от времени. Поскольку уравнение (57) справедливо при любых значениях времени и координат, то правая и левая части его равны постоянной величине, которую обозначим через D.

Таким образом, мы получим два дифференциальных уравнения для определения вида функций U₍τ) и P(x,y,z):

; . (58)

Решением уравнения (58) является

, (59)

где С – постоянная интегрирования.

Постоянная величина D выбирается из физических соображений. В большинстве случаев при нагревании или охлаждении тел по истечении длительного времени температура распределяется в теле определенным образом. Для тепловых процессов, стремящихся к тепловому равновесию, величина D не может быть положительной, потому что можно задать такой промежуток времени, при котором температура в теле будет стремиться к бесконечности, что физически невозможно. Величина D не может равняться нулю, так как при D=0 функция U(τ) в уравнении (59) имела бы постоянное значение, а температура тела не зависела бы от времени, как это следует из уравнения (55), что не реально.

Таким образом, из физических соображений следует, что величина D может быть отрицательной или мнимой величиной. Последний случай будет при условии, что температура тела есть периодическая функция времени, тогда экспонента (59) будет периодической функцией времени.

Рассматривая случай, когда D < 0, предположим, что

, (60)

где а –коэффициент температуропроводности (величина положительная);

m – некоторая постоянная величина, определяемая из граничных условий.

С учетом (60) имеем выражение для функции

. (61)

Уравнение (58) для становится следующим:

(62)

Методы решения уравнения (62) излагаются в курсах высшей математики.

Исходя из того, что при заданных условиях однозначности решение уравнение (62) найдено, и вид функции известен, частное решение уравнения (54) примет вид

(63)

Для общего решения уравнения (54) по принципу наложения берут сумму частных решений. Постоянная m определяется из граничных условий, а постоянная C – из начальных условий.

Метод источников. Метод источников заключается в замене процесса распространения теплоты в теле теплопроводностью совокупностью процессов выравнивания температуры от большого количества элементарных источников теплоты, распределенных в пространстве и времени. Правильный выбор источников теплоты и их распределение во времени – необходимое условие получения надежного решения уравнения теплопроводности.

Сущность метода источников покажем на примере неограниченного тела при одномерном потоке теплоты. В этом случае действие элементарного источника характеризуется функцией источника на бесконечной прямой

. (64)

Функция G представляет температуру в точке x, если в начальный момент времени в точке выделяется теплота в количестве . Количество теплоты на бесконечной прямой равно

(65)

где

. (65а)

Таким образом, количество теплоты Q не зависит от времени. Оно равно произведению площади, ограниченной кривой G и осью абсцисс x, на объемную теплоемкость c_p.

Функцию называют фундаментальным решением уравнения теплопроводности, поскольку она удовлетворяет этому уравнению. В самом деле, для неограниченного тела при одномерном потоке теплоты уравнение (54) имеет вид

. (66)

Если функция G является решением уравнения (66), его можно записать так

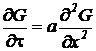. (67)

Пользуясь уравнением (64), найдем выражения для и :

(68)

. (69)

Сопоставление последних двух выражений показывает, что действительно справедливо уравнение (67).

Преобразование Лапласа. Преобразование Лапласа приводит к операционному методу решения линейных и нелинейных дифференциальных уравнений. В этом методе краевые условия используются в начальной стадии решения, что во многих случаях исключает необходимость определения произвольных постоянных.

Преобразование Лапласа функции , обозначаемое символом , называется операцией умножения на с последующим интегрированием по в интервале от 0 до

. (70)

Величина u может быть действительной и мнимой; в обоих случаях ее действительная часть должна быть достаточно велика, чтобы обеспечить сходимость интеграла.

Выражение называется изображением оригинала, т.е. функции . Таким образом, изображения различных функций могут быть получены непосредственным интегрированием. Например, если = , то изображение этой функции будет

. (71)

Обратное изображение дает начальную функцию. Например, называется исходной функцией, или оригиналом изображения .

Преобразования Лапласа первой и второй производных функций определяются соотношениями:

(72)

(73)

В этих изображениях и ее производная представляют граничные условия, которым должна удовлетворять функция .

Интеграл Лапласа (71) и соотношения (72) и (73) можно использовать для интегрирования дифференциальных уравнений.

Метод конечных разностей. Метод конечных разностей часто используют для решения задач нестационарной теплопроводности, особенно при нагревании или охлаждении тел простой геометрической формы. В основе этого метода лежит допущение о возможности замены, например в уравнении теплопроводности, бесконечно малых изменений температуры во времени и пространстве малыми, но конечными ее изменениями. Тем самым протекающий непрерывно процесс изменения температуры в теле при его нагревании или охлаждении заменяется совокупностью скачкообразных процессов.

В случае одномерного нестационарного температурного поля уравнение теплопроводности заменяется уравнением в конечных разностях

. (74)

Решение уравнения (74) может быть выполнено аналитический и графически.

Численный метод. В основу численного метода определения распределения температуры положено уравнение теплопроводности в конечных разностях, с помощью которого вычисляют температуру в фиксированных точках тела. Для применения численного метода рассматриваемое тело разбивают на ряд элементарных объемов, и центральным точкам каждого объема присваивается номер. Предполагается, что тепловые свойства каждого такого объема сосредоточены в его центральной узловой точке и, что передача теплоты между узловыми точками осуществляется через условные теплопроводящие стержни. В нестационарном состоянии в каждом элементарном объеме подвод и отвод теплоты сопровождается изменением внутренней энергии, причем величина этого изменения зависит от изменения температуры в элементарном объеме в течение рассматриваемого промежутка времени, его теплоемкости, плотности и массы.

Рассмотрим применение численного метода к расчету распределения температуры в плоской стенке. Разбивая стенку на элементарные объемы V =δ·δ·1=δ² (рис. 4а,б), где δ – сторона элементарного объема.

Количество теплоты, подводимое к узловой точке в соответствии с законом Фурье, равно . При малой величине δ тепловой поток q можно выразить через конечные разности

а б

Рис. 4. Разбиение и числовая сетка определения нестационарного температурного поля а – одномерное температурное поле; б – двухмерное температурное поле

(75)

где Δ t – разность температур между смежными узловыми точками

Общее количество теплоты за время Δτ равно

(76)

Изменение внутренней энергии в данной узловой точке за время Δτ согласно первому началу термодинамики определяется следующим образом

(77)

где t – температура в рассматриваемой узловой точке в момент времени τ;

– температура в той же точке в момент времени ; V – объем элементарного участка.

Уравнение теплового баланса в конечных разностях для узловой точки 1 (см. рис. 4а) можно записать в виде

. (78)

С учетом (76) уравнение (78) принимает вид

(79)

Разделим уравнение (79) на 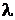и с учетом того, что и - критерий Фурье (безразмерное время) искомая температура в рассматриваемой точке 1 в последующий интервал времени будет равна

. (80)

В случае двухмерного температурного поля тело разбивается на элементарные объемы с размерами ячеек ; расчетная схема узловых точек показана на рис. 4б.

В соответствии с рис. 4б искомое уравнение температуры для точки 5 запишется в виде

. (81)

Уравнения (80 и 81) являются основой численного метода расчета нестационарной теплопроводности одномерного и двухмерного тела.

В качестве примера приведем расчет нестационарной теплопроводности одномерного тела методом разделения переменных.

Не нашли, что искали? Воспользуйтесь поиском: