Охлаждение (нагрев) плоской неограниченной пластины

Рассмотрим неограниченную пластину толщиной 2δ, имеющую в начальный момент времени (τ =0) постоянную по сечению температуру t₀ и помещенную в среду с постоянной температурой t_ж < t₀

Таким образом температурное поле будет одномерным. Кроме того, в

следствии симметрии краевых условий относительно середины стенки температурное поле в любой момент времени будет также симметричным.

В этом случае удобно выбрать за начало координат точку, лежащую посредине между ограничивающими плоскостями пластины, и направить ось х перпендикулярно к поверхности стенки (рис.5).

Дифференциальное уравнение теплопроводности для рассматриваемого случая имеет вид:

; , (82)

где - избыточная температура.

Решая (82) методом разделения переменных частное решение первого уравнения представим в виде

. (83)

Вид функции находится из решения уравнения (62), которое для одномерного температурного поля записывается так:

(84)

Это обыкновенное дифференциальное уравнение имеет частное решение в виде функций .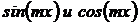

Отсюда частное решение уравнения (83)

(85)

где – произвольная размерная величина; A и B – произвольные постоянные величины частных решений уравнения теплопроводности.

Из условия симметрии задачи следует, что при x=0 величина A =0.

А также, принимая во внимание, что на протяжении всего процесса охлаждения (0<τ<∞) величина не равна нулю (m – положительная размерная величина) частное решение уравнения (85) примет вид

(86)

а общим решение будет

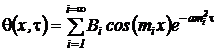. (87)

Значения B и m находятся из граничных условий (82)

, (88)

и

. (88а)

Обозначив 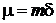и - критерий Био, после ряда преобразований получим трасцендентное уравнение для определения , а следовательно и m

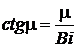. (89)

Значения величин в уравнении (87) находим из начальных условий ,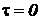

. (90)

Окончательно уравнение распределения температуры в рассматриваемой плоской стенке примет вид

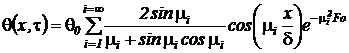. (91)

Расчеты показывают, что в большинстве случаев существенное влияние на значение вычисляемой температуры оказывает несколько первых членов ряда, а для малых значений критерия << 1 точное решение получается даже при одном члене суммы ряда (91).

При x = 0 (середина стенки) имеем

, (92)

при x = ± δ (поверхность стенки)

. (93)

Из анализ уравнения (92 и 93) следует, что температура в центре и на поверхности пластины () зависят только от критериев Bi и Fo. Поэтому для удобства расчетов обычно составляются графики

Рис. 6. Распределение температуры в плоской стенке

а – при Bi → ∞; б – при Bi < 0; в – при 0,1 < Bi < 100

При Bi → ∞ (практически при Bi > 100) температура стенки равна температуре жидкости (рис. 6а), процесс охлаждения определяется свойствами материала стенки (внутренняя задача).

При Bi → 0 (практически при Bi < 0) температура по толщине стенки распределяется равномерно (рис. 6б), процесс охлаждения определяется условиями охлаждения стенки (внешняя задача).

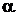При 0,1 < Bi < 100 интенсивность охлаждения стенки зависит как от внутреннего сопротивления , так и от внешнего 1 / (рис 6в).

Количество теплоты на нагревание или отвод теплоты при охлаждении за время τ с обеих сторон определяется уравнением

. (94)

Для единичной площади поверхности стенки

, (95)

где , Dж/м³ – общее количество теплоты за время полного нагревания или охлаждения стенки.

Не нашли, что искали? Воспользуйтесь поиском: