
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Примеры решения задач. Пример 1. Уравнение движения материальной точки вдоль оси имеет вид x=A+Bt+Ct3, где A=2 м, В=1 м/с, С=–0.5 м/с3
Пример 1. Уравнение движения материальной точки вдоль оси имеет вид x=A+Bt+Ct3, где A =2 м, В =1 м/с, С= –0.5 м/с3. Найти координату х, скорость  x и ускорение аx точки в момент времени t =2с.
x и ускорение аx точки в момент времени t =2с.
Решение. Координату х найдем, подставив в уравнение движения числовые значения коэффициентов А, В и С и времени t:
х = (2+1×2 – 0.5 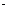 23) м = 0.
23) м = 0.
Мгновенная скорость относительно оси х есть первая производная от координаты по времени:
 .
.
Ускорение точки найдем, взяв первую производную от скорости по времени:
 .
.
В момент времени t = 2с
 x = (1-3×0,5×22) м/с= – 5 м/с; ах = б(— 0,5)×2 м/с2= – 6 м/с2.
x = (1-3×0,5×22) м/с= – 5 м/с; ах = б(— 0,5)×2 м/с2= – 6 м/с2.
Пример 2. Тело вращается вокруг неподвижной оси по закону j=А+Вt+Ct2, где А=10 рад, В =20 рад/с, С= – 2 рад/с2. Найти полное ускорение точки, находящейся на расстоянии r =0,1 м от оси вращения, для момента времени t=4 с.
 Решение. Полное ускорение а точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения аt, направленного по касательной к траектории, и нормального ускорения an, направленного к центру кривизны траектории (рис. 1):
Решение. Полное ускорение а точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения аt, направленного по касательной к траектории, и нормального ускорения an, направленного к центру кривизны траектории (рис. 1):
а = at +an.
Так как векторы ат и аn взаимно перпендикулярны, то модуль ускорения
– 11 –
 . (1)
. (1)
Модули тангенциального и нормального ускорения точки вращающегося тела выражаются формулами аt = er, аn = w2r,
где w – модуль угловой скорости тела; e – модуль его углового ускорения. Подставляя выражения at и ап в формулу (1), находим
 . (2)
. (2)
Угловую скорость w найдем, взяв первую производную угла поворота по времени:  .
.
В момент времени t=4c модуль угловой скорости
w=[20 + 2(-2)4] рад/с = 4 рад/с.
Угловое ускорение найдем, взяв первую производную от угловой скорости по времени:
e=dw/dt = 2С = — 4 рад/с2.
Подставляя значения w, e и r в формулу (2), получаем
а = 0,1  м/с2= 1,65 м/с2.
м/с2= 1,65 м/с2.
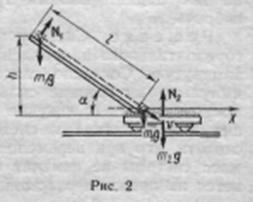 Пример 3. Ящик массой т1 = 20 кг соскальзывает по идеально гладкому лотку длиной l=2 м на неподвижную тележку с песком и застревает в нем. Тележка с песком массой m2=80 кг может свободно (без трения) перемещаться по рельсам в горизонтальном направлении. Определить скорость и тележки с ящиком, если лоток наклонен под углом a=30° к рельсам.
Пример 3. Ящик массой т1 = 20 кг соскальзывает по идеально гладкому лотку длиной l=2 м на неподвижную тележку с песком и застревает в нем. Тележка с песком массой m2=80 кг может свободно (без трения) перемещаться по рельсам в горизонтальном направлении. Определить скорость и тележки с ящиком, если лоток наклонен под углом a=30° к рельсам.
Решение. Тележку и ящик можно рассматривать как систему двух неупруго взаимодействующих тел.
Но эта система не замкнута, так как на нее действуют внешние силы: силы тяжести m1g и m2g и сила реакции N2 (рис. 2). Поэтому применить закон сохранения импульса к системе ящик – тележка нельзя. Но так как проекции указанных сил на направление оси х, совпадающей с направлением рельсов, равны
нулю, то проекцию импульса системы на это направление можно считать
– 54 –
242. Определить среднюю длину свободного пробега 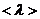 молекулы азота в сосуде вместимостью V=5л. Масса газа m = 0,5 г.
молекулы азота в сосуде вместимостью V=5л. Масса газа m = 0,5 г.
243. Водород находится под давлением р=20мкПа и имеет температуру T=300К. Определить среднюю длину свободного пробега 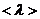 молекулы такого газа.
молекулы такого газа.
244. При нормальных условиях длина свободного пробега 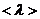 молекулы
молекулы
водорода равна 0,160 мкм. Определить диаметр d молекулы водорода.
245. Какова средняя арифметическая скорость  молекул кислорода при нормальных условиях, если известно, что средняя длина свободного пробега
молекул кислорода при нормальных условиях, если известно, что средняя длина свободного пробега 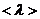 молекулы кислорода при этих условиях равна 100 нм?
молекулы кислорода при этих условиях равна 100 нм?
246. Кислород находится под давлением р=133нПа при температуре T=200К. Вычислить среднее число <z> столкновений молекулы кислорода при этих условиях за время t= 1 с.
247. При каком давлении р средняя длина свободного пробега 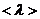 молекул азота равна 1м, если температура газа t=10°С?
молекул азота равна 1м, если температура газа t=10°С?
248. В сосуде вместимостью V=5л находится водород массой m=0,5 г. Определить среднюю длину свободного пробега 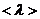 молекулы водорода в этом сосуде.
молекулы водорода в этом сосуде.
249. Средняя длина свободного пробега 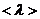 молекулы водорода при некоторых условиях равна 2мм. Найти плотность r водорода при этих условиях.
молекулы водорода при некоторых условиях равна 2мм. Найти плотность r водорода при этих условиях.
250. В сферической колбе вместимостью V=3л, содержащей азот, создан вакуум с давлением р=80мкПа. Температура газа T=250К. Можно ли считать вакуум в колбе высоким? Примечание. Вакуум считается высоким, если длина свободного пробега молекул в нем много больше линейных размеров сосуда.
251Определить количество теплоты Q, которое надо сообщить кислороду объемом V=50л при его изохорном нагревании, чтобы давление газа повысилось на Dр=0,5МПа.
251. При изотермическом расширении азота при температуре T=280К объем его увеличился в два раза. Определить: 1) совершенную при расширении газа работу A; 2) изменение DU внутренней энергии; 3) количество теплоты Q, полученное газом. Масса азота m=0,2кг.
252. При адиабатном сжатии давление воздуха было увеличено от р1=50кПа до
– 53 –
<vкв> а также средние кинетические энергии <eп> поступательного движения молекулы азота и пылинки.
230. Определить среднюю кинетическую энергию <eп> поступательного движения и <eвр> вращательного движения молекулы азота при температуре Т= 400К. Определить также полную кинетическую энергию Eк молекулы при тех же условиях.
231. Определить молярную массу М двухатомной газа и его удельные теплоемкости, если известно, что разность ср — сV удельных теплоемкостей этого газа равна 260 Дж/(кг×К).
232..Найти удельные ср и сV, а также молярные Сp и СV теплоемкости углекислого газа.
233. Определить показатель адиабаты g идеального газа, который при температуре Т=350К и давлении р = 0,4 МПа занимает объем V = 300л и имеет теплоемкость CV=857 Дж/К.
234. В сосуде вместимостью V=6л находится при нормальных условиях двухатомный газ. Определить теплоемкость СV этого газа при постоянном объеме.
235. Определить относительную молекулярную массу Мr и молярную массу М газа, если разность его удельных теплоемкостей ср — cV=2,08 кДж/(кг×К).
236. Определить молярные теплоемкости газа, если его удельные теплоемкости cV=10,4 кДж/(кг×К) и ср= 14,6 кДж/(кг×К).
237. Найти удельные cV и ср и молярные СV и Сp теплоемкости азота и гелия.
238. Вычислить удельные теплоемкости газа, зная что его молярная масса М=4×10-3 кг/моль и отношения теплоемкостей Ср/СV=1,67.
239. Трехатомный газ под давлением р=240кПа и температуре t=20°C занимает объем V=10л. Определить теплоемкость Ср этого газа при постоянном давлении.
240. Одноатомный газ при нормальных условиях занимает объем V=5л. Вычислить теплоемкость этого газа при постоянном объеме.
241. Найти среднее число <z> столкновений за время t=1с и длину свободного пробега 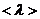 молекулы гелия, если газ находится под давлением р=2кПа при температуре T =200 К.
молекулы гелия, если газ находится под давлением р=2кПа при температуре T =200 К.
– 12 –
постоянной, т. е.
Р1x+ р2x = p`1x + p`2x, (1),
где р1x и р2x – проекции импульса ящика и тележки с песком в момент падения ящика на тележку; p’1x и p'2x – те же величины после падения ящика. Рассматривая тела системы как материальные точки, выразим в равенстве (1) импульсы тел через их массы и скорости, учитывая, что р2x= 0 (тележка до взаимодействия с ящиком покоилась), а также что после взаимодействия оба тела системы движутся с одной и той же скоростью и:
m1  1x = (m1+ т2) и, или m1
1x = (m1+ т2) и, или m1  1 cosa= (m1 +m2) и,
1 cosa= (m1 +m2) и,
где  1– модуль скорости ящика перед падением на тележку;
1– модуль скорости ящика перед падением на тележку;  1x =
1x =  1cosa – проекция этой скорости на ось х.
1cosa – проекция этой скорости на ось х.
Отсюда  (2)
(2)
Модуль скорости  определим из закона сохранения энергии:
определим из закона сохранения энергии:
m1gh = ½ m1  , где h =lsina, откуда
, где h =lsina, откуда
 =
=  .
.
Подставив выражение  в формулу (2), получим
в формулу (2), получим

После вычислений найдем
 м/c.
м/c.
Пример 4. При выстреле из пружинного пистолета вертикально вверх пуля массой m=20 г поднялась на высоту h=5 м. Определить жесткость k пружины пистолета, если она была сжата на ∆ х=10 см. Массой пружины и силами трения пренебречь.
Решение. Рассмотрим систему пружина – пуля. Так как на тела системы действуют только консервативные силы, то для решения задачи можно применить закон сохранения энергии в механике. Согласно ему полная механическая энергия E системы в начальном состоянии (в данном случае перед выстрелом)
– 13 –
равна полной энергии Е в конечном состоянии (когда пуля поднялась на высоту h), т.е.
Е1=Е2, или Т1+П1=Т2+П2, (1)
где Т1, Т2, П1 и П2 – кинетические и потенциальные энергии системы в начальном и конечном состояниях.
Так как кинетические энергии пули в начальном и конечном состояниях равны нулю, то равенство (1) примет вид
П1=П2. (2)
Примем потенциальную энергию пули в поле сил тяготения Земли, когда пуля покоится на сжатой пружине, равной нулю, а высота подъема пули будет отсчитываться от торца сжатой пружины. Тогда энергия системы в начальном состоянии будет равна потенциальной энергии сжатой пружины, т.е. П1= ½ k(∆x) 2, а в конечном состоянии – потенциальной энергии пули на высоте h, т.е. П2=mgh.
Подставив выражения П1 и П2 в формулу (2), найдем ½ k(∆x)2 =mgh, откуда
k=2mgh/x2. (3)
Проверим, дает ли полученная формула единицу жесткости k. Для этого в правую часть формулы (3) вместо величин подставим их единицы (единицу какой-либо величины принято обозначать символом этой величины, заключенным в квадратные скобки):
 (1кг×1м×с-2×1м)/1м2=(1кг×м×с-2)/1м=1Н/м.
(1кг×1м×с-2×1м)/1м2=(1кг×м×с-2)/1м=1Н/м.
Убедившись, что полученная единица является единицей жесткости (1Н/м), подставим в формулу (3) значения величин и произведем вычисления:

Пример 5. Шар массой m1, движущийся горизонтально с некоторой скоростью 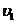 , столкнулся с неподвижным шаром массой m2. Шары абсолютно упругие, удар прямой, центральный. Какую долю e своей кинетической энергии первый шар передал второму?
, столкнулся с неподвижным шаром массой m2. Шары абсолютно упругие, удар прямой, центральный. Какую долю e своей кинетической энергии первый шар передал второму?
– 52 –
Dр=100кПа. Определить массу т израсходованного кислорода. Процесс считать изотермическим.
220. Определить плотность r водяного пара, находящегося под давлением р=2,5кПа и имеющего температуру Т=250 К.
221. Определить внутреннюю энергию U водорода, а также среднюю кинетическую энергию <e> молекулы этого газа при температуре Т = 300К, если количество вещества n этого газа равно 0,5 моль.
222. Определить суммарную кинетическую энергию EK поступательного движения всех молекул газа, находящегося в сосуде вместимостью V=3л под давлением p=540 кПа.
223. Количество вещества гелия n= 1,5 моль, температура Т= 120 К. Определить суммарную кинетическую энергию Eк поступательного движения всех молекул этого газа.
224. Молярная внутренняя энергия Um некоторого двухатомного газа равна
6,02 кДж/моль. Определить среднюю кинетическую энергию <eвр> вращательного движения одной молекулы этого газа. Газ считать идеальным.
225. Определить среднюю кинетическую энергию <eвр> одной молекулы водяного пара при температуре Т =500 К.
226. Определить среднюю квадратичную скорость <vкв> молекулы газа, заключенного в сосуд вместимостью V=2л под давлением р=200кПа. Масса газа m=0,3 г.
227. Водород находится при температуре T=300 К. Найти среднюю кинетическую энергию <eвр> вращательного движения одной молекулы, а также суммарную кинетическую энергию Eк всех молекул этого газа; количество водорода n=0,5моль.
228. При какой температуре средняя кинетическая энергия <eп> поступательного движения молекулы газа равна 4,14×10-21 Дж?
229. В азоте взвешены мельчайшие пылинки, которые движутся так, как если бы они были очень крупными молекулами. Масса каждой пылинки равна 6×10-10 г. Газ находится при температуре T=400 К. Определить средние квадратичные скорости
– 51 –
208. В баллоне вместимостью V=3л содержится кислород массой m=10г. Определить концентрацию молекул газа.
209. Определить относительную молекулярную массу Мr. 1) воды; 2) углекислого газа; 3) поваренной соли.
210. Определить количество вещества n и число N молекул азота массой т = 0,2 кг.
211. В цилиндр длиной l=1, 6м, заполненный воздухом при нормальном атмосферном давлении р0, начали медленно вдвигать поршень площадью основания S= 200 см2. Определить силу F, действующую на поршень, если его остановить на расстоянии l1=10см от дна цилиндра.
212. В баллоне находится газ при температуре Т1=400К. До какой температуры Т2 надо нагреть газ, чтобы его давление увеличилось в 1,5 раза?
213. Баллон вместимостью V=20л заполнен азотом при температуре 7=400 К. Когда часть газа израсходовали, давление в баллоне понизилось на Dp = 200кПа. Определить массу m израсходованного газа. Процесс считать изотермическим.
214. В баллоне вместимостью V=15л находится аргон под давлением р1=600кПа и при температуре T1 = 300 К. Когда из баллона было взято некоторое количество газа, давление в баллоне понизилось до p2= 400кПа, а температура установилась Т2=260 К. Определить массу m аргона, взятого из баллона.
215. Два сосуда одинакового объема содержат кислород. В одном сосуде давление р1 = 2 МПа и температура T1 = 800K, в другом р2 = 2,5 МПа, T2 = 200К. Сосуды соединили трубкой и охладили находящийся в них кислород до температуры T=200 К. Определить установившееся в сосудах давление р.
216. Вычислить плотность r азота, находящегося баллоне под давлением р=2МПа и имеющего температуру Т =400 К.
217. Определить относительную молекулярную массу Мr газа, если при температуре T=154К и давлении р=2,8МПа он имеет плотность r=6,1 кг/м3.
218. Найти плотность азота r при температуре Т=400К и давлении р=2МПа.
219. В сосуде вместимостью V=40 л находится кислород при температуре T=300К. Когда часть газа израсходовали, давление в баллоне понизилось на
– 14 –
Решение. Доля энергии, переданной первым шаром второму, выразится соотношением
 (1)
(1)
где Т1 – кинетическая энергия первого шара до удара; u2 и Т2 –скорость и кинетическая энергия второго шара после удара.
Как видно из формулы (1), для определения e надо найти u2. Согласно условию задачи, импульс системы двух шаров относительно горизонтального направления не изменяется и механическая энергия шаров в другие виды не переходит. Пользуясь этим, найдем:
M1  =m1u1+m2u2; (2)
=m1u1+m2u2; (2)
 (3)
(3)
Решив совместно уравнения (2) и (3) найдем  :
:

Подставив это выражение u2 в формулу (1) и сократив на 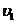 и m1, получим
и m1, получим
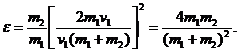
Из найденного соотношения видно, что доля переданной энергии зависит только от масс сталкивающихся шаров.
 Пример 6. Через блок в виде сплошного диска, имеющего массу m=80г (рис. 4), перекинута тонкая гибкая нить, к концам которой подвешены грузы с массами m1 =100г и m2 =200г. Определить ускорение, с которым будут двигаться грузы, если их предоставить самим себе. Трением и массой нити пренебречь.
Пример 6. Через блок в виде сплошного диска, имеющего массу m=80г (рис. 4), перекинута тонкая гибкая нить, к концам которой подвешены грузы с массами m1 =100г и m2 =200г. Определить ускорение, с которым будут двигаться грузы, если их предоставить самим себе. Трением и массой нити пренебречь.
Решение. Рассмотрим силы, действующие на каждый груз и на блок в отдельности. На каждый груз действуют две силы: сила тяжести и сила упругости (сила натяжения нити). Направим ось х вертикально
– 15 –
вниз и напишем для каждого груза уравнение движения (второй закон Ньютона) в проекциях на эту ось. Для первого груза
T1 - m1g = m1a (1)
для второго груза
m2g - T 2 = m2a (2)
Под действием моментов сил T1 и T2 относительно оси z, перпендикулярной плоскости чертежа и направленной за чертеж, блок приобретает угловое ускорение e. Согласно основному уравнению динамики вращательного движения,
 , (3)
, (3)
где  ;
;  – момент инерции блока (сплошного диска) относительно оси z.
– момент инерции блока (сплошного диска) относительно оси z.
Согласно третьему закону Ньютона, с учетом невесомости нити 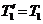 ,
,  . Воспользовавшись этим, подставим в уравнение (3) вместо
. Воспользовавшись этим, подставим в уравнение (3) вместо  и
и 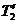 выражения Т1 и Т2, получив их предварительно из уравнений (1) и (2):
выражения Т1 и Т2, получив их предварительно из уравнений (1) и (2):
(m2g-m2a)r-(m1g+m1a)r=mr2a/(2r).
После сокращения на r и перегруппировки членов найдем
 (4)
(4)
Формула (4) позволяет массы m1, m2 и m выразить в граммах, как они даны в условиях задачи, а ускорение – в единицах СИ. После подстановки числовых значений в формулу (4) получим

Пример 7. Маховик в виде сплошного диска радиусом R=0,2м и массой m=50 кг раскручен до частоты вращения n1=480 мин-1 и предоставлен сам
себе. Под действием сил трения маховик остановился через t=50c. Найти момент М сил трения.
Решение. Для решения задачи воспользуемся основным уравнением динамики вращательного движения в виде
 (1)
(1)
– 50 –
 Па = 3,2 Па;
Па = 3,2 Па;
A=2×3,14×(0,1)2×40×10-3 Дж = 2,5×10-3 Дж = 2,5 мДж.
Не нашли, что искали? Воспользуйтесь поиском: