Контрольная работа 2

Таблица вариантов

201. Определить количество вещества v и число N молекул кислорода массой m=0,5 кг.

202. Сколько атомов содержится в ртути: 1) количеством вещества n = 0,2 моль; 2) массой m=1 г?

203. Вода при температуре t=4°C занимает объем V=1см³. Определить количество вещества n и число N молекул воды.

204. Найти молярную массу М и массу m _м одной молекулы поваренной соли.

205. Определить массу m _M одной молекулы углекислого газа.

206. Определить концентрацию п молекул кислорода, находящегося в сосуде вместимостью V=2л. Количество вещества n кислорода равно 0,2моль.

207. Определить количество вещества n водорода, заполняющего сосуд объемом V=3л, если концентрация молекул газа в сосуде n=2×10¹⁸ м^-3.

– 49 –

ними силами. График процесса приведен на рис. 8.

Пример 11. Тепловая машина работает по обратимому циклу Карно. Температура теплоотдатчика Т₁=500 К. Определить термический КПД h цикла и температуру Т₂ теплоприемника тепловой машины, если за счет каждого кило джоуля теплоты, полученной от теплоотдатчика, машина совершает работу А=350 Дж.

Решение. Термический КПД тепловой машин показывает, какая доля теплоты, полученной от теплоотдатчика, превращается в механическую работу. Термический КПД выражается формулой

h=A/Q₁,

где Q₁ — теплота, полученная от теплоотдатчика, А - работа, совершенная рабочим телом тепловой машины. Зная КПД цикла, можно по формуле

h=(T₁ – T₂)/T₁ определить температуру охладителя Т₂:

Произведем вычисления:

h = 350/1000 =0,35; T₂ = 500(1 - 0,35) К = 325 К.

Пример 12. Найти добавочное давление внутри мыльного пузыря диаметром d=10 cм. Какую работу нужно совершить, чтобы выдуть этот пузырь?

Решение. Пленка мыльного пузыря имеет две сферические поверхности: внешнюю и внутреннюю. Обе поверхности оказывают давление на воздух, заключенного внутри пузыря. Так как толщина пленки чрезвычайно мала, то диаметры обеих поверхностей практически одинаковы. Поэтому добавочное давление

где радиус пузыря. Так как r=d/2, то p = 8a/d.

Работа, которую нужно совершить, чтобы, растягивая пленку, увеличить ее поверхность на DS, выражается формулой A = aDS, или A = a(S — So). В данном случае S — общая площадь двух сферических поверхностей пленки мыльного пузыря; So — общая площадь двух поверхностей плоской пленки, затягивавшей отверстие трубки до выдувания пузыря. Пренебрегая So, получаем

A=aS=2pd²a.

Произведем вычисления:

– 16 –

где М_г –момент внешних сил (в данном случае момент сил трения), действующих на маховик относительно оси z, J_z –момент инерции маховика относительно оси z; Dw – изменение угловой скорости маховика за время .

Момент инерции маховика в виде сплошного диска определяется по формуле

Изменение угловой скорости Dw=w₂-w₁ выразим через конечную n₂ и начальную п₁ частоты вращения, пользуясь соотношением w = 2pn:

Dw=w₂-w₁ =2pn₂-2pn₁=2p(n₂-n₁).

Подставив в формулу (1) выражения J_z и Dw, получим

M_z=pmR²(n₂-n₁)/Dt. (2)

Проверим, дает ли расчетная формула единицу момента силы (Н×м). Для этого в правую часть формулы вместо символов величин подставим их единицы:

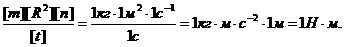
Подставим в (2) числовые значения величин и произведем вычисления, учитывая, что n₁ =480мин^-1=480/60с^-1 = 8с^-1:

Знак минус показывает, что момент сил трения оказывает на маховик тормозящее действие.

Пример 8. Платформа в виде сплошного диска радиусом R=1,5 м и массой m₁=180 кг вращается около вертикальной оси с частотой n=10 мин^-1. В центре платформы стоит человек массой m₂=60 кг. Какую линейную скорость 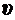относительно пола помещения будет иметь, человек, если он перейдет на край платформы?

Решение. Согласно условию задачи, момент внешних сил относительно оси вращения z, совпадающей с геометрической осью платформы, можно считать равным нулю. При этом условии проекция L_z момента импульса системы платформа – человек остается постоянной:

– 17 –

L_z=J_zw = const, (1)

где J_z – момент инерции платформы с человеком относительно оси z; w – угловая скорость платформы. Момент инерции системы равен сумме моментов инерции тел, входящих в состав системы, поэтому в начальном состоянии J_z=J₁+J₂, а в конечном состоянии .

С учетом этого равенство (1) примет вид

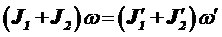(2)

где значения моментов инерции J₁ и J₂ платформы и человека соответственно относятся к начальному состоянию системы; и – к конечному.

Момент инерции платформы относительно оси z пpи переходе человека не изменяется

Moмент инерции человека относительно той же оси будет изменяться.

Если рассматривать человека как материальную точку, то его момент инерции J₂ в начальном состоянии (в центре платформы) можно считать равным нулю. В конечном состоянии (на краю платформы) момент инерции человека J₂’=m₂R². Подставим в формулу (2) выражения моментов инерции, начальной угловой скорости вращения платформы с человеком (w = 2pn) и конечной угловой скорости ( = /R, где – скорость человека относительно пола) ( m₁R²+0) 2pn = ( m₁R² + m₂R²) /R.

После сокращения на R² и простых преобразований находим скорость:

= 2pnRm₁ /(m₁+2m₂).

Произведем вычисления:

Пример 9. Ракета установлена на поверхности Земли для запуска в

вертикальном направлении. При какой минимальной скорости 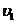, сообщенной ракете при запуске, она удалится от поверхности на расстояние, равное радиусу

– 48 –

объем в n₁=5 раз, а затем был сжат изотермически, причем объем газа уменьшился в n₂=5 раз. Найти температуру в конце адиабатного расширения и работу, совершаемую газом при этих процессах. Изобразите процесс графически.

Решение. Температуры и объемы газа, совершающего адиабатный процесс, связаны между собой соотношением

или

где g — отношение теплоемкостей газа при постоянном давлении и постоянном объеме; n₁=V₂/V₁.

Отсюда получаем следующее выражение для конечной температуры:

Работа А₁ газа при адиабатном расширении может быть определена по формуле

где С_V — молярная теплоемкость газа при постоянном объеме. Работа А₂ газа при изотермическом процессе может быть выражена в виде

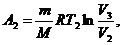или

где n₂= V₂/Vз.

Произведем вычисления, учитывая, что для водорода как двухатомного газа g=1, 4, i=5 и М=2×10^{- 3} кг/моль: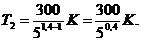

Так как 5^0,4=1,91 (находится логарифмированием), то

Дж = 29,8 кДж;

Дж=-21 кДж.

Знак минус показывает, что при сжатии работа газа совершается над газом внеш

– 47 –

Q=DU+A.

Произведем вычисления, учтя, что для кислорода M=32×10^-3 кг/моль (см. табл. 6 приложения):

;

;

Дж = 0,400×10⁶ Дж = 0,4 МДж;

A=A₁=0,4 МДж;

Дж=3,24×10⁶Дж=3,24МДж;

Q=(3,24+0,4)МДж=3,64МДж.

График процесса приведен на рис. 7.

Рис. 7

Пример 10. В цилиндре под поршнем находится водород массой m=0,02 кг при температуре T₁=300K. Водород сначала расширился адиабатно, увеличив свой

– 18 –

Земли (R = 6.37×10⁶ м)? Всеми силами, кроме силы гравитационного взаимодействия ракеты и Земли, пренебречь.

Решение: Со стороны Земли на ракету действует сила тяжести, являющаяся потенциальной силой. При неработающем двигателе под действием потенциальной силы механическая энергия ракеты изменяться не будет. Следовательно.

Т₁ + П₁ = Т₂ + П₂, (1)

где Т₁, П₁ и Т₂, П ₂ – кинетическая и потенциальная энергии ракеты после выключения двигателя в начальном (у поверхности Земли) и конечном (на расстоянии, равном радиусу Земли) состояниях. Согласно условию задачи П₁=0, Т₂=0, T₁= m ² / 2, П₂=mgR. Следовательно, и .

Пример 10. Точка совершает гармонические колебания с частотой v=10Гц. В момент, принятый за начальный, точка имела максимальное смещение: x_max= 1 мм. Написать уравнение колебаний точки и начертить её график.

x = Asin(wt + j₁), (1)

где А – амплитуда колебаний; w – циклическая частота, t – время; j₁ – начальная фаза.

По определению, амплитуда колебаний A = x_max. (2)

Циклическая частота w связана с частотой n соотношением

w = 2pn, (3)

Для момента времени t=0 формула (1) примет вид x_max= Asinj₁, откуда начальная фаза

j₁ = arcsin = arcsin 1, или j₁=(2k+l)×p/2 (k= 0, 1, 2,...).

E=0,1мДж. Определить амплитуду А колебаний и наибольшее значение силы F_max, действующей на частицу.

Решение. Для определения амплитуды колебаний воспользуемся выражением полной энергии частицы:

Е = ½ mw²A²,

где w = 2p/Т. Отсюда амплитуда

(1)

Так как частица совершает гармонические колебания, то сила, действующая на нее, является квазиупругой и, следовательно, может быть выражена соотношением F= – kx, где k – коэффициент квазиупругой силы; х – смещение колеблющейся точки. Максимальной сила будет при максимальном смещении x_max равном амплитуде:

F_max=kA. (2)

Коэффициент k выразим через период колебаний:

k = mw²=m4p² /T². (3)

Подставив выражения (1) и (3) в (2) и произведя упрощения, получим

.

– 46 –

Рассуждая так же, получим формулу для вычисления дельной теплоемкости смеси при постоянном давлении:

c_p=c_p,1w₁+c_p,₂w₂

Произведем вычисления:

c_V=(6,24×10²×0,8+1,04×10⁴×0,2)Дж/(кг×К)=2,58×10³Дж/(кг×К) =2,58 кДж/(кг×К);

_Cp=(l,04×10³×0,8+1,46×10⁴×0,2)Дж/(кг×К)=3,75×10³ Дж/(кг×К)=3,75 кДж/(кг×К).

Пример 9. Кислород массой m=2кг занимает объем V₁=1м³ и находится под давлением p₁=0,2МПа. Газ был нагрет сначала при постоянном давлении до объема V₂=3м³, а затем при постоянном объеме до давления р₃=0,5МПа. Найти изменение DU внутренней энергии газа, совершенную им работу А и теплоту Q, переданную газу. Построить график процесса.

Решение. Изменение внутренней энергии газа

(1)

где i — число степеней свободы молекул газа (для двухатомных молекул кислорода i=5); DT=T₃ -Т₁ — разность температур газа в конечном (третьем) и начальном состояниях.

Начальную и конечную температуру газа найдем из уравнения Менделеева — Клапейрона pV= , откуда

T=pVM/(mR).

Работа расширения газа при постоянном давлении выражается формулой

Работа газа, нагреваемого при постоянном объеме равна нулю:

A₂=0.

Следовательно, полная работа, совершаемая газом,

А=А₁+А₂=А₁.

Согласно первому началу термодинамики, теплота переданная газу, равна сумме изменения внутренней энергии DU и работы А:

– 45 –

где i — число степеней свободы молекулы газа; М — молярная масса. Для неона (одноатомный газ) i=3 и М=20×10^-3 кг/моль (см. табл. 6 приложения).

Произведем вычисления:

6,24×10² Дж/(кг×К);

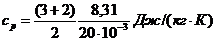=1,04×10³ Дж/(кг×К).

Для водорода (двухатомный газ) i=5 и M=2×10^-3 кг/моль. Тогда

1,04×10⁴ Дж/(кг×К);

1,46×10⁴ Дж/(кг×К)

Пример 8. Вычислить удельные теплоемкости c_V и с_p смеси неона и водорода, если массовые доли неона и водорода составляют w₁=80% и w₂=20%. Значения удельных теплоемкостей газов взять из предыдущего примера.

Решение. Удельную теплоемкость c_V смеси при постоянном объеме найдем следующим образом. Теплоту необходимую для нагревания смеси на DТ выразим двумя способами:

Q=c_V(m₁+m₂)DT,

Q=(c_V,1m₁+c_V,2m₂)DT,

где c_V,1 — удельная теплоемкость неона; c_V,2 — удельная теплоемкость водорода.

Приравняв правые части (1) и (2) и разделив обе части полученного равенства на DТ, получим с_V(m₁+m₂)=c_V,1m₁+c_V,2m₂. Отсюда

или

с_V=c_V,1w₁+c_V,2w_2,

где и .

– 20 –

Произведем вычисления:

Пример 12. Складываются два колебания одинакового направления, выраженные уравнениями

где A₁ = 3см, A₂ =2см, t₁, = 1/6с, t₂=1/3с, T = 2с. Построить векторную диаграмму сложения этих колебаний и написать уравнение результирующего колебания.

Решение. Для построения векторной диаграммы сложения двух колебаний одного направления надо фиксировать какой-либо момент времени. Обычно векторную диаграмму строят для момента времени t = 0. Преобразовав оба уравнения к канонической форме x=Acos(wt+j), получим

Отсюда видно, что оба складываемых гармонических колебания имеют одинаковую циклическую частоту

w = 2p/T.

Начальные фазы первого и второго колебаний соответственно равны

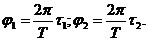
Произведем вычисления:

– 21 –

Изобразим векторы a₁ и А₂. Для этого отложим от резки длиной А₁ = 3 см и А₂ = 2 см под углами j₁= 30° в j₂=60° к оси Ох. Результирующее колебание будет происходить с той же частотой w и амплитудой А, равной

геометрической сумме амплитуд a₁ и A₂: A = A₁ +A₂ Согласно теореме косинусов,

Начальную фазу результирующего колебания можно также определить непосредственно из векторной диаграммы (рис 6):

Произведем вычисления:

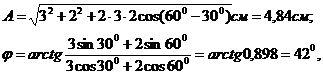
или j=0,735 рад.

Рис.6.

Так как результирующее колебание является гармоническим, имеет ту же частоту, что и слагаемые колебания, то его можно записать в виде

x=Acos(wt+j) где A = 4.84см, w = 3,14 с^-1, j-=0,735рад.

Пример 13. Плоская волна распространяется вдоль прямой со скоростью = 20 м/с. Две точки, находящиеся на этой прямой на расстояниях x₁=12м и x₂ = 15м от источника волн, колеблются с разностью фаз Dj=0,75p. Найти длину волны l написать уравнение волны и найти смешение указанных точек в момент t=1,2 с, если амплитуда колебаний A = 0,1 м.

Решение: Точки, находящиеся друг от друга на расстоянии, равном длине волны l, колеблются с разностью фаз, равной 2p; точки, находящиеся друг от друга на любом расстоянии Dx, колеблются с разностью фаз, равной

Dj = Dx×2p/l = (x₂-x₁) ×2p/l..

Решая это равенство относительно l, получаем

l=2p(x₂-x₁)/Dj. (1)

– 44 –

Решение. На каждую степень свободы молекулы газа приходится одинаковая средняя энергия <e_i> = ½ kT,

N_A — постоянная Авогадро; n — количество вещества.

Если учесть, что количество вещества n = т/М, где m — масса газа; М — молярная масса газа, то формула примет вид

Подставив выражение N в формулу (2), получаем

Е_к= N_Am <e_вр>/M (4)

Произведем вычисления, учитывая, что для кислорода M=32×10^-3 кг/моль (см. табл. 6 приложения):

Пример 7. Вычислить удельные теплоемкости при постоянном объеме с_V и при постоянном давлении c_p неона и водорода, принимая эти газы за идеальные.

Решение. Удельные теплоемкости идеальных газов; выражаются формулами

– 43 –

Паскаль является единицей давления. Произведем вычисления по формуле (5), учитывая, что М= 4×10^-3 кг/моль (см. табл. 6 приложения):

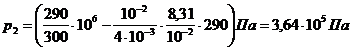= 0,364 МПа.

Пример 5. Баллон содержит т₁ = 80 г кислорода и m₂ = 320 г аргона. Давление смеси р=1МПа, температура Т = 300 К. Принимая данные газы за идеальные определить объем V баллона.

Решение. По закону Дальтона, давление смеси равно сумме парциальных давлений газов, входящих в состав смеси. По уравнению Менделеева — Клапейрона, парциальные давления р₁ кислорода и р₂ аргона выражаются формулами:

P₁ = m₁RT/(M₁V), p₂ = m₂RT/(M₂V).

Следовательно, по закону Дальтона, давление cмеси газов

p=p₁+p₂, или

откуда объем баллона

(1)

Произведем вычисления, учитывая, что M₁=32×10^-3 кг/моль, M₂=40×10^-3 кг/моль (см. табл. 6 приложения):

Пример 6. Найти среднюю кинетическую энергию <e_вр> вращательного движения одной молекулы кислорода при температуре Т=350 К, а также кинетическую энергию E_к вращательного движения всех молекул кислорода массой m = 4 г.

– 22 –

Подставив числовые значения величин, входящих в выражение (1), и выполнив арифметические действия, получим

Для того чтобы написать уравнение плоской волны надо еще найти циклическую частоту w. Так как w=2p/T (T=l/ – период колебаний), то w=2pv/l.

Произведем вычисления:

Зная амплитуду А колебаний, циклическую частоту w и скорость v распространения волны, можно написать уравнение плоской волны для данного случая:

y=Acosw(t-x/ ), (2)

где А=0,1 м, w=5pс^-1, =20 м/c.