МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИ КА

Основные формулы

Количество вещества (число молей) системы:

n = N/N_A,

где N – число (молекул, атомов, ионов и т. п.), составляющих тело (систему); N_A – постоянная Авогадро (N_А=6,02×10²³ моль^-1). Молярная масса вещества

М = m/n,

где m – масса тела; n – количество вещества этого тела.

Относительная молекулярная масса вещества

где n_i – число атомов i-ro химического элемента, входящих в состав молекулы данного вещества; А_r,i – относительная атомная масса этого элемента. Количество вещества – число структурных элементов (молекул, атомов, ионов и т. п.), содержащихся в теле или системе. Количество вещества выражается в молях. Моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде-12 массой 0,012 кг. Атомные массы приводятся в таблице Д. И. Менделеева. (См. также табл. 6 приложения).

Связь молярной массы М сотносительной молекулярной массой вещества.

М = M_rk,

где k=10^-3 кг/моль.

Количество вещества смеси газов

n=n₁+n₂+…+ n_n=N₁/N_A+ N₂/N_A+…+ N_n/N_A

или

n=m₁/M₁+ m₂/M₂+…+ m_n/M_n

где n _i – количество вещества,. N_i - число молекул, m_i - масса, M_i - молярная масса i- гoкомпонента смеси.

Уравнение Менделеева – Клапейрона (уравнение состояния идеального газа)

,

где т – масса газа, М – молярная масса газа, R – универсальная газовая

– 33 –

175. Определить период Т простых гармонических колебаний диска радиусом R = 40 см около горизонтальной оси, проходящей через образующую диска.

176. Определить период Т колебаний математического маятника, если его модуль максимального перемещения Dr=18 см и максимальная скорость .

177. Материальная точка совершает простые гармонические колебания так, что в начальный момент времени смещение x₀=4 см, а скорость . Определить амплитуду А и начальную фазу j₀ колебаний, если их период Т=2 с.

178. Складываются два колебания одинакового на­ правления и одинакового периода: х₁=А₁ sinw₁t и x₂=A₂sinw₂(t +t), где A₁=A₂=3см, w₁= w₂=pс^-1, t=0.5 с. Определить амплитуду А и начальную фазу j₀ результирующего колебания. Написать его уравнение. Построить векторную диаграмму для момента времени t=0.

179. На гладком горизонтальном столе лежит шар массой М=200 г, прикрепленный к горизонтально расположенной легкой пружине с жесткостью k=500Н/м. В шар попадает пуля массой т=10 г, летящая со скоростью 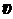=300 м/с, и застревает в нем. Пренебрегая перемещением шара во время удара и сопротивлением воздуха, определить амплитуду А ипериод Т колебаний шара.

180. Шарик массой m=60 г колеблется с периодом T=2 с. В начальный момент времени смещение шарика x₀=40см и он обладает энергией E=0,02Дж. Записать уравнение простого гармонического колебания шарика и закон изменения возвращающей силы с течением времени.

– 32 –

167. Спутник обращается вокруг Земли по круговой орбите на высоте h=520км. Определить период обращения спутника. Ускорение свободного падения g у поверхности Земли и ее радиус R считать известными.

168. Определить линейную и угловую скорости спутника Земли, обращающегося по круговой орбите на высоте h=1000 км. Ускорение свободного падения g у поверхности Земли и ее радиус R считать известными.

169. Какова масса Земли, если известно, что Луна в течение года совершает 13 обращений вокруг Земли и расстояние от Земли до Луны равно 3,84×10⁸ м?

170. Во сколько раз средняя плотность земного вещества отличается от средней плотности лунного? Принять, что радиус R_З Земли в 390 раз больше радиуса R_Л Луны и вес тела на Луне в 6 раз меньше веса тела на Земле.

171. На стержне длиной l=30 см укреплены два оди­наковых грузика: один – в середине стержня, другой – на одном из его концов. Стержень с грузами колеблется около горизонтальной оси, проходящей через свободный конец стержня. Определить приведенную длину L и период Т простых гармонических колебаний данного физического маятника. Массой стержня пренебречь.

172. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых x=A₁sinw₁t и y=A₂cosw₂t, где A₁=8см, A₂=4см, w₁ = w₂=2 с^-1. Написать уравнение траектории и построить ее. Показать направление движения точки.

173. Точка совершает простые гармонические колебания, уравнение которых x=Asinwt, где A=5см, w= 2с^-1. В момент времени, когда точка обладала потенциальной энергией П=0,1 мДж, на нее действовала воз­вращающая сила F=5 мН. Найти этот момент времени t.

174. Определить частоту n простых гармонических колебаний диска радиусом R=20 см около горизонтальной оси, проходящей через середину радиуса диска перпендикулярно его плоскости.

Не нашли, что искали? Воспользуйтесь поиском: