Контрольная работа 1

Таблица вариантов

– 23 –

101. Тело брошено вертикально вверх с начальной скоростью м/с. Когда оно достигло верхней точки полета из того же начального пункта, с той же начальной скоростью , вертикально вверх брошено второе тело. На каком расстоянии h от начального пункта встретятся тела? Сопротивление воздуха не учитывать.

102. Материальная точка движется прямолинейно с ускорением а=5м/с². Определить, на сколько путь, пройденный точкой в п -ю секунду, будет больше пути, пройденного в предыдущую секунду. Принять = 0.

103. Две автомашины движутся по дорогам, угол между которыми a=60° Скорость автомашин =54 км/ч и =72км/ч. С какой скоростью удаляются машины одна от другой?

104. Материальная точка движется прямолинейно с начальной скоростью =10м/с и постоянным ускорением а= – 5м/с². Определить, во сколько раз путь Ds, пройденный материальной точкой, будет превышать модуль ее перемещения спустя t=3с после начала отсчета времени.

105. Велосипедист ехал из одного пункта в другой. Первую треть пути он проехал со скоростью =18 км/ч. Далее половину оставшегося времени он ехал со скоростью =22 км/ч, после чего до конечного пункта он шел пешком со скоростью =5 км/ч. Определить среднюю скорость < > велосипедиста.

106. Тело брошено под углом a=30° к горизонту со скоростью =30м/с. Каковы будут нормальное а_n, тангенциальное а_t ускорения тела через время t= 1c после начала движения?

107. Материальная точка движется по окружности с постоянной угловой скоростью w=p/6 рад/с. Во сколько раз путь Ds, пройденный точкой за время t=4с, будет больше модуля ее перемещения ? Принять, что в момент начала отсчета времени радиус-вектор r, задающей положение точки на окружности, относительно исходного положения был повернут на угол j₀=p/3рад.

108. Материальная точка движется в плоскости xy согласно уравнениям

x =A₁+B₁t+C₁t² и у = A₂+B₂t+C₂t², где В₁=7м/с, C₁= – 2м/с², В₂= – 1м/с,

m₁ =m/n_a (1).

Подставив в (1) значения М и N_A, найдем массу молекулы воды:

Если молекулы воды плотно прилегают друг к другу, то можно считать, что на каждую молекулу приходится объем (кубическая ячейка) V₁=d³, где d — диаметр молекулы. Отсюда

(2)

Объем V₁ найдем, разделив молярный объем V_m начисло молекул в моле, т.е. на n_a:

(3)

Подставим выражение (3) в (2):

^, где V_m=M/r. Тогда

(4)

Проверим, дает ли правая часть выражения (4) единицу длины:

Произведем вычисления:

– 24 –

С₂=0,2 м/с². Найти модули скорости и ускорения точки в момент времени t = 5с.

109. По краю равномерно вращающейся с угловой скоростью w=1 рад/с платформы идет человек и обходит платформу за время t= 9,9с. Каково наибольшее ускорение а движения человека относительно Земли! Принять радиус платформы R = 2м.

110. Точка движется по окружности радиусом R = 30 см с постоянным угловым ускорением e. Определить тангенциальное ускорение а_t точки, если известно, что за время t=4c она совершила три оборота и в конце третьего оборота ее нормальное ускорение а_n=2,7 м/с².

111. При горизонтальном полете со скоростью =250 м/с снаряд массой т=8 кг разорвался на две части. Большая часть массой m₁ = 6 кг получила скорость u₁= 400 м/с в направлении полета снаряда. Определить модуль и направление скорости и₂ меньшей части снаряда.

112. С тележки, свободно движущейся по горизонтальному пути со скоростью =3 м/с, в сторону, противоположную движению тележки, прыгает человек, после чего скорость тележки изменилась и стала равной u₁=4 м/с. Определить горизонтальную составляющую скорости u₂ человека при прыжке относительно тележки. Масса тележки m₁ = 210 кг, масса человека m₂=70 кг.

113. Орудие, жестко закрепленное на железнодорожной платформе, производит выстрел вдоль полотна железной дороги под углом a=30° к линии горизонта. Определить скорость u₂ отката платформы, если снаряд вылетает со скоростью u₁ =480 м/с. Масса платформы с орудием и снарядами m₂=18 масса снаряда т₁ =60 кг.

114. Человек массой m₁=70 кг, бегущий со скоростью =9км/ч, догоняет тележку массой m₂=190кг, движущуюся со скоростью =3,6 км/ч, и вскакивает на нее. С какой скоростью станет двигаться тележка с человеком? С какой скоростью будет двигаться тележка с человеком, если человек до прыжка бежал навстречу тележке?

115. Конькобежец, стоя на коньках на льду, бросает камень массой т₁=2,5 кг под

– 25 –

углом a= 30° к горизонту со скоростью = 10м/с. Какова будет начальная скорость движения конькобежца, если масса его m₂=60 кг? Перемещением конькобежца во время броска пренебречь.

116. На полу стоит тележка в виде длинной доски, снабженной легкими колесами. На одном конце доски стоит человек. Масса его т₁ = 60 кг, масса доски m₂ = 20 кг. С какой скоростью (относительно пола) будет двигаться тележка, если человек пойдет вдоль нее со скоростью (относительно доски) =1м/с? Массой колес и трением пренебречь.

117. Снаряд, летевший со скоростью = 400 м/с, в верхней точке траектории разорвался на два осколка. Меньший осколок, масса которого составляет 40% от массы снаряда, полетел в противоположном направлении со скоростью u₁ = 150 м/с. Определить скорость и₂ большего осколка.

118. Две одинаковые лодки массами т = 200 кг каждая (вместе с человеком и грузами, находящимися в лодках) движутся параллельными курсами навстречу друг другу с одинаковыми скоростями =1м/с. Когда лодки поравнялись, то с первой лодки на вторую и со второй на первую одновременно перебрасывают грузы массами т₁ = 200 кг. Определить скорости u₁ и u₂ лодок после перебрасывания грузов.

119. На сколько переместится относительно берега лодка длиной l=3,5 м и массой m₁=200кг, если стоящий на корме человек массой т₂=80кг переместится на нос лодки? Считать лодку расположенной перпендикулярно берегу.

120. Лодка длиной l=3м и массой т=120кг стоит на спокойной воде. На носу и корме находятся два рыбака массами т₁=60кг и т₂= 90кг. На сколько сдвинется лодка относительно воды, если рыбаки поменяются местами?

121. В деревянный шар массой m₁ =8кг, подвешенный на нити длиной l=1,8 м, попадает горизонтально летящая пуля массой m₂ = 4г. С какой

скоростью летела пуля, если нить с шаром и застрявшей в нем пулей отклонилась от вертикали на угол a = 3°? Размером шара пренебречь. Удар пули считать прямым, центральным.

– 40 –

Пример 2. Определить молярную массу М смеси кислорода массой m₁=25 и азота массой m₂=75г.

Решение. Молярная масса смеси М есть отношение массы смеси m к количеству вещества смеси n:

M = m/n. (1)

Масса смеси равна сумме масс компонентов смеси:

т = m₁+m₂

Количество вещества смеси равно сумме количеств вещества компонентов:

Подставив в формулу (1) выражения m и n, получим

(2)

Молярные массы кислорода M₁ и азота М₂ равны:

М₁ = 32×10^-3 кг/моль; М₂ = 28×10^-3 кг/моль.

Подставим значения величин в (2) и произведем вычисления:

= 28,9×10^-3 кг/моль.

Пример 3. Определить число N молекул, содержащихся в объеме

V=1 мм³ воды, и массу m₁ молекулы воды. Считая условно, что молекулы воды имеют вид шариков, соприкасающихся друг с другом, найти диаметр d молекул.

Решение: Число N молекул, содержащихся в некоторой системе массой m, равно произведению постоянной Авогадро N_A на количество вещества n:

N = n / n_a

Так как n=m/M, где М — молярная масса, то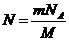

Выразив в этой формуле массу как произведение плотности на объем V, получим N =rVN_A/M.

– 39 –

где d – расстояние между плоскостями.

Не нашли, что искали? Воспользуйтесь поиском: