
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Координаты в пространстве.
Определение. Пусть в пространстве заданы три координатные оси OX, OY и OZ с некомпланарными ортами 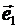 ,
, 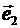 ,
,  соответственно. Тогда четверка (0,
соответственно. Тогда четверка (0, 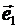 ,
, 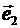 ,
,  ) называется афинным репером, или афинной системой координат в пространстве.
) называется афинным репером, или афинной системой координат в пространстве.
Точка 0 - начало координат, векторы 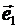 ,
, 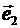 ,
,  - базисные векторы.
- базисные векторы.
Так как векторы 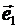 ,
, 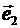 ,
,  - линейно независимы, то для
- линейно независимы, то для
любого вектора  имеет место разложение:
имеет место разложение:
 = x
= x 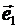 + y
+ y 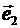 + z
+ z 
Числа x, y, z называются координатами точки М (записывается: М (х, у, z)),  называется радиус-вектором точки М с координатами х, у, z (записывается:
называется радиус-вектором точки М с координатами х, у, z (записывается:  = (х, у, z)), причем х называется абсциссой, у - ординатой, z - аппликатой.
= (х, у, z)), причем х называется абсциссой, у - ординатой, z - аппликатой.
Афинную систему часто обозначают через OXYZ. Оси OX, OY, OZ называют соответственно осями абсцисс, ординат и аппликат. Плоскости, определяемые координатными осями, т.е. OXY, OYZ, OXZ, называют координатными плоскостями. Эти плоскости делят все пространство на восемь частей, называемых координатными октантами.
Если упорядоченная тройка векторов 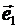 ,
, 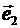 ,
,  является правой, то афинную систему называют правой, в противном случае - левой. В дальнейшем под афинной системой будем понимать правую систему. Если базисные векторы
является правой, то афинную систему называют правой, в противном случае - левой. В дальнейшем под афинной системой будем понимать правую систему. Если базисные векторы 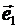 ,
, 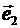 ,
,  попарно взаимно ортогональны, то афинная система координат называется декартовой (прямоугольной), а базисные векторы обозначается соответственно
попарно взаимно ортогональны, то афинная система координат называется декартовой (прямоугольной), а базисные векторы обозначается соответственно 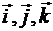 .
.
В частности, если даны точки А (х 1, у 1, z 1), В (х 2, у 2, z 2), то
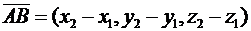
Векторы  = (х1,у1,z1) и
= (х1,у1,z1) и  = (х2,у2,z2) коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, т.е.
= (х2,у2,z2) коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, т.е.

Не нашли, что искали? Воспользуйтесь поиском: