II. Сечение в виде прямоугольного треугольника

1. Осевые моменты инерции относительно взаимно перпендикулярных осей x0y (совпадающих со сторонами треугольника)

Для определения момента инерции относительно оси х выделим элементарную площадку в виде полоски бесконечно малой ширины dу, параллельной оси х, на расстоянии у от нее (см. рис.). Площадь площадки . Длину полоски b(y) определим из подобия треугольников с основаниями b(y) и b,

откуда .

Тогда . Подставляя это выражение в (*) и устанавливая пределы интегрирования «0- h», получим

.

Аналогично определяется I_y.

2. Центробежный момент инерции относительно осей x0y (совпадающих со сторонами треугольника)

Центробежный момент инерции, согласно определению, равен

.

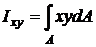Используем ту же элементарную площадку, что и ранее (см. рис.). В качестве координаты х примем координату центра тяжести элементарной площадки

.

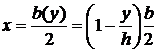Подставляем это выражение, а также формулу для dA под интеграл и интегрируем в пределах от 0 до h

Таким образом, формулы для моментов инерции сечения, в виде прямоугольного треугольника, относительно осей, совпадающих с катетами, имеют вид

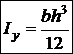, , . (23)

Заметим, что для рассматриваемого сечения больший интерес представляют моменты инерции относительно центральных осей (ЦО), параллельных катетам треугольника.

3. Моменты инерции относительно взаимно перпендикулярных ЦО x_ссy_с (параллельных сторонам треугольника)

Формулы для моментов инерции прямоугольного треугольника относительно осей x_ссy_с (см. рис.) легко получить, используя выражения (23), а также теорему о параллельном переносе осей, согласно которой:

осевые моменты инерции ; ;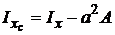

центробежный момент инерции .

Здесь: а, е – координаты центра тяжести сечения в системе координат x0y

, , .

Подставляя эти выражения, а также соотношения (23) в приведенные выше формулы, получим

(24)

Отметим, что ориентация сечения относительно осей оказывает влияние на знак центробежного момента инерции. Для рассматриваемой ориентации оказалось, что <0. Действительно, на рис. видно, что большая часть сечения лежит в области с отрицательным произведением координат х ´ у (вторая и четвертая координатные четверти). Это и обусловливает отрицательный знак полученного центробежного момента инерции. Ниже приведены схемы с различной ориентацией прямоугольного треугольника относительно ЦО, параллельных сторонам, для которых указан знак .

Поскольку знак может быть как положительным, так и отрицательным, формулу для центробежного момента инерции относительно ЦО, параллельных сторонам треугольника, запишем в виде

. (24-а)

Заметим также, что приведенные схемы могут использоваться при определении знака центробежного момента инерции стандартных уголковых профилей.

Не нашли, что искали? Воспользуйтесь поиском: