Положение главных осей и значения главных моментов инерции сечений

Проведем анализ соотношений (12) с целью определения:

- положения главных осей;

- положения осей, относительно которых осевые моменты инерции сечения экстремальны;

- значений главных и экстремальных осевых моментов инерции сечений.

Поскольку, по определению, центробежный момент инерции сечения относительно главных осей равен нулю, положение главных осей определим, приравняв нулю последнее из соотношений (12) ( )

.

В этом уравнении угол a* определяет положение главных осей. Разделим уравнение на cos2 a*, и определим полученную при этом тригонометрическую функцию угла a*

. (13)

Уравнение (13) имеет бесчисленное множество корней (a*; a* +90°; a* +180°; a* +270°;…), которые определяют только две взаимно перпендикулярных главных оси с углами наклона a* и a* +90°.

Для определения положения осей, относительно которых осевые моменты инерции экстремальны, возьмем производную по a от первого из соотношений (12)

Производная по a от имеет такой же вид, но с обратным знаком.

Отметим, что выражение, стоящее в скобках, представляет собой центробежный момент инерции сечения относительно повернутых осей . Приравнивая производную нулю и вводя обозначение a = a*, получим в результате решения уравнения формулу (13).

Отсюда следует важный вывод о том, что оси, относительно которых осевые моменты инерции сечения экстремальны, являются главными осями. Это позволяет расширить определение главных осей: главные оси – это взаимно перпендикулярные оси, относительно которых центробежный момент инерции сечения равен нулю, а осевые моменты инерции экстремальны. Естественно, что это касается только совокупности осей, проходящих через одну точку. Поскольку таких главных осей только две, очевидно, что относительно одной из осей главный момент инерции сечения будет максимальным (I _max), относительно другой – минимальным (I _min).

Обозначим главные оси через u и v. Для определения значений главных моментов инерции сечения (I_u и I_v) в формулу для (12) необходимо подставить выражения для a* и a* +90°. К такому же результату придем, если подставим a* в формулы (12) для и

(14)

(15)

Преобразуем (14), используя тригонометрические соотношения

, , получим

Исключим из последнего выражения центробежный момент инерции , используя формулу (13), согласно которой

.

После соответствующей подстановки получим

Перепишем полученный результат, используя тригонометрическое

преобразование , а также подстановку (13),

Внося множитель перед скобкой под радикал, окончательно будем иметь

Если выполнить такие же подстановки и выкладки для I_v, получится точно такая же формула. Заметим, что эта формула дает значения для двух главных моментов инерции I _max и I _min. Очевидно, что знак «+» соответствует I _max, знак «–» – I _min. В этой связи формулу для главных моментов инерции сечения целесообразно записать в виде

. (16)

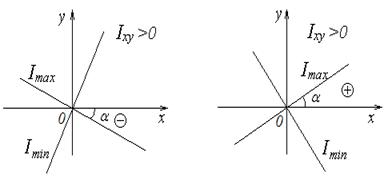
Таким образом, углы a* и a* +90°, определяющие положение главных осей, мы вычисляем по формуле (13), а значения осевых моментов инерции относительно этих осей (главных моментов) – по формуле (16). При этом остается не установленным – относительно какой из двух осей момент инерции будет максимальным, относительно какой – минимальным? Здесь удобно пользоваться следующим правилом: если центробежный момент сечения в исходных осях положительный (I_xy >0), ось, соответствующая I _max, проходит через II и IV четверти исходных координат, если отрицательный (I_xy <0) – через I и III четверти (см. рис.).

Еще раз отметим, что главные оси, сами по себе, интереса, с точки зрения сопротивления материалов, не представляют. Важно научиться определять положение главных осей среди «семейства» центральных осей, т.е. определять положение главных центральных осей, а также значения соответствующих им главных центральных моментов инерции сечения.

Завершая этот подраздел, напомним о теореме инвариантности суммы осевых моментов инерции сечения относительно взаимно перпендикулярных осей, проходящих через одну точку. Естественно, что эта теорема распространяется и на главные моменты инерции

. (17)

Не нашли, что искали? Воспользуйтесь поиском: