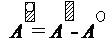Некоторые теоремы об основных ГХС

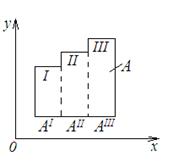
Теорема I (сложения) – момент инерции сложного сечения, относительно некоторой оси, равен сумме моментов инерции, относительно той же оси, простых фигур, составляющих рассматриваемое сложное сечение.

Доказательство. Рассмотрим сложное нестандартное сечение, которое можно разбить на три простых фигуры – три прямоугольника (см. рис.). Тогда площадь сложной фигуры можно представить в виде , где Аⁱ – площадь простой «i» фигуры.

Момент инерции произвольного сечения относительно оси х определяется выражением

.

Этот интеграл можно представить как сумму трех таких же интегралов, интегрирование каждого из которых проводится по площади простых фигур, составляющих сложное сечение

.

В свою очередь, каждый из трех записанных выше интегралов представляет собой, по определению, момент инерции относительно оси х простых фигур, на которые разбито сложное сечение

.

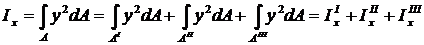В общем случае для сечения, состоящего из п простых фигур, будем иметь

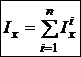. (8)

Эта теорема справедлива для всех основных ГХС (А, S_x, S_y, I_x, I_y, I_xy, I_r) и может быть использована как при сложении, так и при вычитании. Например, если заданное сечение имеет отверстие (см. рис.), то момент инерции такого сечения будет определяться как разность момента инерции прямоугольника и соответствующего момента инерции отверстия.

Ix = Ix - Ix

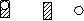
Эта теорема широко используется при определении ГХ сложных сечений.

Теорема II (свойство инвариантности суммы осевых моментов инерции относительно взаимно ортогональных осей) – сумма осевых моментов инерции сечения относительно взаимно перпендикулярных осей – величина постоянная, не зависит от угловой ориентации координатных осей с общим началом и равна полярному моменту инерции сечения относительно начала координат.

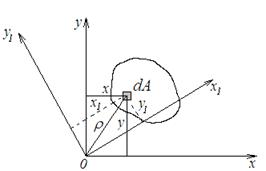
Доказательство. Используя систему координат х0у в качестве исходной, запишем, согласно определению, сумму осевых моментов инерции относительно осей х и у

.

Переменная интегрирования и ее пределы у интегралов одинаковы, поэтому объединяем подынтегральные выражения

.

Учитывая, что х² + у² = r², а , будем иметь

. (*)

Повернем исходную систему координат относительно начала (точки «0») на произвольный угол, получим систему х₁0у₁, в которой координаты бесконечно малого элемента – х₁ и у₁. Записывая аналогично сумму осевых моментов инерции относительно взаимно перпендикулярных осей х₁ и у₁, получим

. (**)

Сравнивая (*) и (**), окончательно будем иметь

. (9)

Эта теорема используется при определении осевых и полярного моментов инерции простых и сложных сечений. Из теоремы также следует, что экстремальные (максимальное и минимальное) значения осевых моментов инерции произвольного сечения относительно всевозможных осей, проходящих через одну точку, будут реализоваться относительно взаимно перпендикулярных осей.

Теорема III (о параллельном переносе осей) – осевой момент инерции относительно оси, которая параллельна центральной оси, равен сумме осевого момента инерции относительно центральной оси и произведения площади сечения на квадрат расстояния между осями.

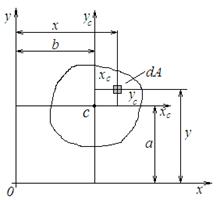
Доказательство. Имеем две системы декартовых координат: исходную (х0у) и центральную (х_сСу_с), соответствующие оси которых параллельны друг другу. Расстояния между осями, а, точнее, координаты центра тяжести сечения в исходных осях (a и b) могут быть как положительными, так и отрицательными.

Выразим координаты элементарной площадки dА в исходных осях через координаты в центральных осях и расстояния между осями

. (*)

Запишем выражение для момента инерции относительно оси х и выполним подстановку (*)

.

Учитывая, что (как статический момент относительно центральной оси), окончательно будем иметь

.

Формулы для I_y и I_хy выводится аналогично.

Таким образом, формулы для моментов инерции при параллельном переносе осей имеют вид

. (10)

Из этой теоремы следует важный вывод: минимальный осевой момент инерции из всевозможного набора параллельных осей будет относительно центральной оси.

Теорема IV (об изменении направления одной из осей) – при изменении направления одной из осей на противоположное, центробежный момент инерции сечения меняет знак.

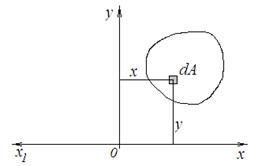
Доказательство. Изменим направление оси х на противоположное. Тогда . (*)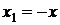

Запишем выражение для центробежного момента инерции относительно осей х₁0у и используем подстановку (*)

.

Таким образом, получили

. (11)

Не нашли, что искали? Воспользуйтесь поиском: