Статические моменты (моменты площади) сечения

; <=>0 [длина³]. (2)

Если известны координаты центра тяжести сечения , , статические моменты можно определять по формулам

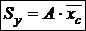; . (3)

Если известны статические моменты сечения относительно некоторых осей, можно определить в этих осях координаты центра тяжести рассматриваемого сечения.

(4)

Оси, проходящие через центр тяжести сечения, называют центральными осями (x _c, y _c).

Центральных осей у фигуры (сечения) произвольной формы может быть бесчисленное множество.

Статические моменты относительно центральных осей равны 0.

;

3. Осевые моменты инерции сечения (относительно осей x, y)

; >0 (длина⁴) (5)

4. Центробежный момент инерции сечения (относительно пары взаимно перпендикулярных осей x, y)

<=>0 (длина⁴) (6)

Взаимно перпендикулярные оси, относительно которых центробежный момент инерции равен нулю, называются главными осями, а осевые моменты инерции относительно этих осей – главными моментами инерции сечения.

Для сечения произвольной формы любые две взаимно перпендикулярные оси, начало которых размещается в произвольной точке пространства, всегда можно преобразовать в главные оси путем поворота их относительно начала координат на определенный угол. Таким образом, главных осей у фигуры произвольной формы – бесчисленное множество.

Главные оси, проходящие через центр тяжести сечения (либо центральные оси, относительно которых центробежный момент инерции равен нулю), называются главными центральными осями, а осевые моменты инерции относительно этих осей – главными центральными моментами инерции сечения. Сечение произвольной формы имеет только одну пару главных центральных осей.

5. Полярный момент инерции сечения (относительно полюса – начала координат)

>0 (длина⁴) (7)

Не нашли, что искали? Воспользуйтесь поиском: