Некоторые сведения о главных центральных осях сечений

Учитывая важность понятия «главные центральные оси (ГЦО)» приведем некоторые сведения об этих осях, которые не требуют каких-либо сложных доказательств.

1. Если сечение имеет одну ось симметрии, одна из ГЦО совпадает с осью симметрии, другая ГЦО ортогональна оси симметрии и проходит через центр тяжести.

Рассмотрим равнобедренный треугольник, у которого ось у ₀ является осью симметрии, а ось х ₀ перпендикулярна к оси симметрии и проходит через центр тяжести сечения «с». Очевидно, что оси х ₀ су ₀ являются центральными. Введем также ось х^/ ₀, противоположного к оси х ₀ направления.

Заметим, что часть сечения I в системе координат х ₀ су ₀ зеркально симметрична части II в системе координат х^/ ₀ су ₀, откуда следует

.

Согласно теореме IV, имеет место равенство

либо с учетом первого выражения .

Центробежный момент инерции всего сечения, согласно теореме сложения, запишется в виде

.

Используя предыдущее выражение, получим

.

Поскольку центробежный момент инерции относительно взаимно перпендикулярных центральных осей х ₀ су ₀ равен нулю, эти оси являются также и главными.

Ниже приведены примеры сечений с одной осью симметрии.

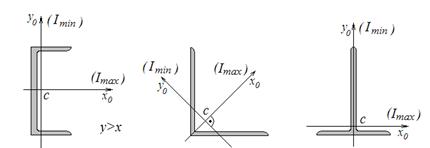
Здесь же указано, относительно каких ГЦО реализуются максимальные (I _max) и минимальные (I _min) главные центральные моменты инерции (ГЦМ) сечения. Заметим, что, согласно определению, сечение всегда вытянуто вдоль той ГЦО, относительно которой величина ГЦМ минимальна.

2. Если сечение имеет две оси симметрии, то обе оси симметрии являются ГЦО.

3. Если сечение имеет более двух осей симметрии, то все центральные оси являются ГЦО, причем значения ГЦМ относительно всех ГЦО одинаковы.

Докажем это на примере квадратного сечения, которое имеет 4 оси симметрии.

Введем исходные оси х ₀ су ₀, которые являются осями симметрии и, согласно положению, являются ГЦО. Повернем эти оси на произвольный угол a и докажем, что полученные путем поворота оси х ₁ су ₁ также являются ГЦО, т.е. 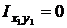, а также, что ГЦМ относительно всех ГЦО одинаковы, т.е.

.

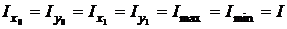Запишем выражение для центробежного момента инерции при повороте координатных осей

.

Учитывая, что , а 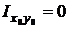, получим 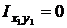, т.е. взаимно перпендикулярные центральные оси x ₁ cy ₁ являются ГЦО.

Определим, при тех же условиях, момент инерции относительно оси х₁

.

Учитывая, что угол a является произвольным, можно утверждать

.

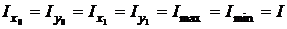К сечениям высокой степени симметрии относятся круг, кольцо, равносторонние правильные, выпуклые многоугольники, а также другие сложные нестандартные, стандартные и комбинированные сечения.

Не нашли, что искали? Воспользуйтесь поиском: