Моменты инерции сечения при повороте координатных осей

Имеем две системы декартовых координат: исходную – х0у и развернутую на произвольный угол a относительно начала координат – х ₁ 0у ₁ (см. рис.). Считая моменты инерции относительно исходных осей х0у (I_x, I_y, I_xy), а также угол поворота осей a (положителен при повороте против часовой стрелки) заданными, определим моменты инерции сечения относительно повернутых осей х ₁ 0у ₁ ().

Выразим координаты элементарной площадки dА в развернутой системе координат через координаты исходной системы. Согласно рисунку,

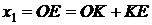, где , ,

, где , .

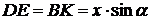Подставляя значения отрезков в исходные формулы, получим

(*)

В соответствие с определением, момент инерции относительно оси х ₁

.

Используем для у ₁ подстановку (*) и, разворачивая выражение в скобках, получим

Выносим за знак интеграла тригонометрические функции и используем преобразование 2sin a cos a = sin2 a. В результате будем иметь

.

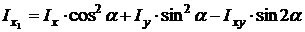Аналогично поступаем при получении остальных характеристик относительно развернутых осей

.

Таким образом, соотношения между моментами инерции сечения при повороте координатных осей относительно начала координат имеют вид

(12)

Из полученных соотношений (12) видно, что при изменении угла a будут изменяться значения моментов инерции сечения. Причем, если величины осевых моментов будут изменяться в пределах положительных значений (от минимального до максимального значений), центробежный момент инерции будет менять также и знак. Соотношения (12) дают возможность определить максимальные и минимальные значения осевых моментов инерции, а также положение главных центральных осей.

Отметим одно важное обстоятельство. С точки зрения сопротивления материалов, из всех возможных осей интерес представляют, в основном, только главные центральные оси и соответственно главные центральные моменты инерции сечения.

Не нашли, что искали? Воспользуйтесь поиском: