Теорема Шаля для отрезков. Координата направленного отрезка, заданного двумя точками декартовой оси координат. Расстояние между двумя точками, лежащими на оси координат

Теорема (1) Шаля. (Для отрезков). Если А, В, С три любые точки оси, то . (Число число 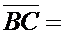числу ).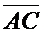

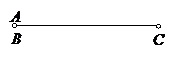
Доказательство. (1). Предположим, что точки А, В, С попарно различны. Если точки В лежит между точками А и С, то длина отрезка АС равна сумме длин отрезков АВ и ВС:

;

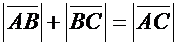но так как в рассматриваемом случае направленные отрезки 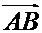, и и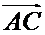меют одинаковое направление, то числа , 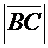и имеют один и тот же знак, а потому

.

__________________________________________

(2). Если точка С лежит между А и В, то

__________________________________________

(3). Если точка А лежит между точками В и С, то , т.е.

; но ,

В А С имеем .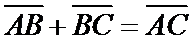

__________________________________________

(4). Если точки А и В совпадают, то

(5). Если точки В и С совпадают, то .

_________________________________________

(6). Наконец если точки А и С

совпадают, то

.

Теорема 2. Координата направленного отрезка заданного двумя точками и 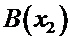оси координат, вычисляются по формуле

Доказательство. На основании теоремы Шаля , откуда

.

Теорема 3. Расстояние d между точками и оси координат вычисляется по формуле

Эта теорема является следствием предыдущей.

Не нашли, что искали? Воспользуйтесь поиском: