Деление направленного отрезка в данном отношении

Пусть на одной и той же прямой лежат два направленных отрезка 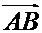и , причем невырожденный направленный отрезок. Тогда отношение в случае, если направленный отрезок также невырожденный, называется число , абсолютная величина которого равна 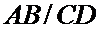и которое положительно, если и имеют одинаковое направление, и отрицательно в противном случае. Если отрезок вырожденный, а отрезок невырожденный, то будем считать, что . Если отрезок вырожденный, то отношение 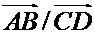не определяется.

Если отношение к равно , то пишут .

Пусть на некоторой прямой задан невырожденный направленный отрезок и путь С – какая-нибудь точка этой прямой, отличная от точки В.

Отношением, в котором точка С делит невырожденный направленный отрезок , называется число , определяемое соотношением .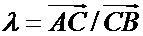

Из этого определения следует, что 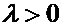, если точка С лежит между

А В точками А и В, и 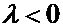в противном случае.

При этом , если точка А лежит между

точками В и С.

B C

И , если точка В лежит между точками А и С.

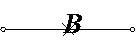А С

Заметим, что отношение, в котором точка С делит невырожденный направленный отрезок 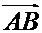, никогда не равно -1.

Теорема 4. Если на оси координат заданы две различные точки и и, если точка делит направленный отрезок 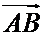в отношении , то

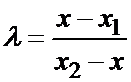; и

Доказательство. Из данного определения отношения , в котором точка С делит невырожденный направленный отрезок 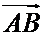, а также из определения координаты направленного отрезка, лежащего на оси, следует

значит на основании теоремы 2 § 4 (то,что координата направленного отрезка 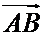заданного двумя точками и 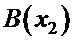оси координат, вычисляются по формуле 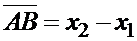), имеем: , откуда .

Следствие. Координата середины отрезка равна полусумме координат его концов: 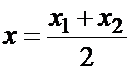. В самом деле: для середины отрезка .

Определение. Простым отношением (АВС) трех точек А, В, С лежащих на одной прямой и взятых в определенном порядке (А, В, С) называется число , равное

,

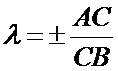причем перед дробью ставится знак «+», если точка С лежит между А и В, и знак «-» в противном случае.

Определение. Сложным, или ангармоническим, отношением четырех точек А, В, С, D, лежащих на одной прямой (точки А и В различны, С и D различны), называется число

Если =-1, то говорят, что точка С и D гармонически разделены точками А и В.

Теорема 5. Каково бы ни было число , существует и притом только одна точка С, которая делит невырожденный направленный отрезок в отношении .

Доказательство. Введем на прямой АВ систему координат. Предполагая, что некоторая точка С (х) делит направленный отрезок в отношении , на основании предыдущей теоремы найдем

,

где 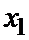и - координаты точек А и В. Этим доказана единственность точки С, делящей направленный отрезок 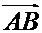в данном отношении , т.е. доказано, что если такая точка существует, то только одна.

Далее, точка С с координатой

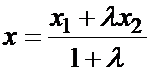
делит направленный отрезок в отношении , так как из написанного соотношения следует

Точки С и В различны, так как разность их координат не равна нулю; в самом деле,

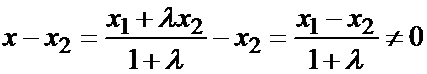(т.к. это но поскольку по условию теоремы отрезок невырожденный).

Поэтому и из последнего равенства следует, что

.

Не нашли, что искали? Воспользуйтесь поиском: