
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Преобразование системы координат на прямой
1. Преобразование системы координат на прямой.
Пусть на прямой линии введены 2 системы координат с одним и тем же положительным направлением и одним и тем же масштабным отрезком. Пусть О – начало координат одной из

них (назовем ее старой), а  - начало координат
- начало координат
другой (назовем ее новой). Пусть М – произвольная точка прямой, пусть х – координата точки М в старой системе (будем называть ее старой координатой). Пусть  - координата точки М в новой системе (назовем ее новой координатой). Пусть
- координата точки М в новой системе (назовем ее новой координатой). Пусть  - координата нового начала в старой системе.
- координата нового начала в старой системе.
Тогда по теореме Шаля имеет место равенство  , т.е.
, т.е.  или
или  , т.е. старая координата точки М равна новой координате этой точки, сложенной с координатой нового начала в старой системе.
, т.е. старая координата точки М равна новой координате этой точки, сложенной с координатой нового начала в старой системе.
Такое преобразование системы координат называется переносом системы координат.
Из равенства 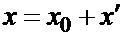 вытекает, что
вытекает, что  (это выражение новой координаты через старую).
(это выражение новой координаты через старую).
При переносе системе координат координата направленного отрезка не меняется.
Векторы
В настоящем параграфе дается определение вектора в трехмерном евклидовом пространстве (понятия вектора на плоскости и вектора на прямой являются частными случаями этого определения). Предварительно введем ряд дополнительных определений.
Два невырожденных направленных отрезка  и
и  называются коллинеарными, если прямые АВ и СD или параллельны, или совпадают. Вырожденный направленный отрезок считается коллинеарным любому направленному отрезку.
называются коллинеарными, если прямые АВ и СD или параллельны, или совпадают. Вырожденный направленный отрезок считается коллинеарным любому направленному отрезку.
 Будем говорить, что два невырожденных направленных отрезка
Будем говорить, что два невырожденных направленных отрезка 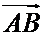 и
и  , лежащих на параллельных прямых, имеют одинаковое направление, если точки В и D лежат по одну сторону от прямой АС. Если точки В и D лежат по разные сторон от прямой АС, то направленные отрезки
, лежащих на параллельных прямых, имеют одинаковое направление, если точки В и D лежат по одну сторону от прямой АС. Если точки В и D лежат по разные сторон от прямой АС, то направленные отрезки  и
и  имеют противоположное направление (см.рис.3). В случае, если невырожденные направленные отрезки
имеют противоположное направление (см.рис.3). В случае, если невырожденные направленные отрезки  и
и  лежат на одной прямой а, они имеют одинаковое направление, если на любой прямой b, параллельной а, найдется невырожденный направленный отрезок
лежат на одной прямой а, они имеют одинаковое направление, если на любой прямой b, параллельной а, найдется невырожденный направленный отрезок  , имеющий одинаковое направление с каждым из направленных отрезков
, имеющий одинаковое направление с каждым из направленных отрезков 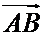 и
и  . Если же любой неврожденный отрезок
. Если же любой неврожденный отрезок  (лежащий на прямой b, параллельной прямой а имеет одинаковое направление с одним из направленных отрезков
(лежащий на прямой b, параллельной прямой а имеет одинаковое направление с одним из направленных отрезков  или
или  и противоположное с другим, то направленные отрезки
и противоположное с другим, то направленные отрезки 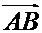 и
и  имеют противоположное направление. Наконец, условимся считать, что вырожденный направленный отрезок имеет одинаковое направление с любым направленным отрезком.
имеют противоположное направление. Наконец, условимся считать, что вырожденный направленный отрезок имеет одинаковое направление с любым направленным отрезком.
Если направленные отрезки  и
и  коллинеарны, то будем писать
коллинеарны, то будем писать  ; если при этом они имеют одинаковое направление, то
; если при этом они имеют одинаковое направление, то  , а если противоположное, то
, а если противоположное, то  .
.
Два направленных отрезка 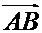 и
и  называются равными
называются равными  , если выполнены следующие условия:
, если выполнены следующие условия:
1) равны длины отрезков  и
и  ;
;
2) направленные отрезки  и
и  коллинеарны;
коллинеарны;
3) направленные отрезки  и
и  имеют одинаковое направление.
имеют одинаковое направление.
Свободным вектором  называется класс всех равных между собой направленных отрезков. Нулевым вектором называется класс всех вырожденных направленных отрезков.
называется класс всех равных между собой направленных отрезков. Нулевым вектором называется класс всех вырожденных направленных отрезков.
Свободный вектор  часто обозначают и изображают любым из направленных отрезков
часто обозначают и изображают любым из направленных отрезков  того класса направленных отрезков, которым является вектор
того класса направленных отрезков, которым является вектор  .
.
Отложить свободный вектор  от точки А – значит построить направленный отрезок
от точки А – значит построить направленный отрезок 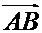 входящий в класс направленных отрезков, образующих вектор
входящий в класс направленных отрезков, образующих вектор  .
.
В дальнейшем под словом «вектор» мы будем понимать свободный вектор.
Рассмотрим два произвольных вектора  и
и  . Пусть
. Пусть  направленный отрезок из класса направленных отрезков, образующих вектор
направленный отрезок из класса направленных отрезков, образующих вектор  , а
, а  – направленный отрезок из класса направленных отрезков, образующих вектор
– направленный отрезок из класса направленных отрезков, образующих вектор  .
.
Векторы  и
и  называются коллинеарными, если коллинеарны направленные отрезки
называются коллинеарными, если коллинеарны направленные отрезки 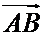 и
и  . Если при этом направленные отрезки
. Если при этом направленные отрезки  и
и  имеют одинаковое направление, то векторы
имеют одинаковое направление, то векторы  и
и  имеют одинаковое направление, а если направленные отрезки
имеют одинаковое направление, а если направленные отрезки 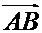 и
и  имеют противоположное направление, то векторы
имеют противоположное направление, то векторы  и
и  имеют противоположное направление.
имеют противоположное направление.
Если векторы  и
и  коллинеарны, то будем писать
коллинеарны, то будем писать  ; если при этом они имеют одинаковое направление, то будем писать
; если при этом они имеют одинаковое направление, то будем писать  , а если противоположное, то
, а если противоположное, то  . Если направленные отрезки
. Если направленные отрезки  и
и  равны, то будем говорить, что векторы
равны, то будем говорить, что векторы  и
и  равны, и писать
равны, и писать  . Длиной или модулем вектора
. Длиной или модулем вектора  называется длина отрезка АВ.
называется длина отрезка АВ.
Длина вектора обозначается так:  .
.
Теорема 6. Необходимым и достаточным условием равенства направленных отрезков  и
и  является совпадение середины отрезка АD с серединой отрезка ВС.
является совпадение середины отрезка АD с серединой отрезка ВС.
Доказательство необходимости. Дано  . Требуется доказать, что середина отрезка АD совпадает с серединой отрезка ВС.
. Требуется доказать, что середина отрезка АD совпадает с серединой отрезка ВС.
Пусть О – середина отрезка АD.
Рассмотрим преобразование S симметрии относительно точки О. При этом преобразовании каждой точке М ставится в соответствие точка  , симметричная точке М относительно точки О, т.е. такая, что точка О является серединой отрезка
, симметричная точке М относительно точки О, т.е. такая, что точка О является серединой отрезка  . Каждый направленный отрезок
. Каждый направленный отрезок  при преобразовании S переходит в направленный отрезок
при преобразовании S переходит в направленный отрезок  , такой, что
, такой, что  (рис. 4).
(рис. 4).
 Пусть
Пусть  – точка, в которую при преобразовании S перейдет точка В. Так как точка А переходит в точку D, то направленный отрезок
– точка, в которую при преобразовании S перейдет точка В. Так как точка А переходит в точку D, то направленный отрезок 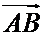 перейдет в направленный отрезок
перейдет в направленный отрезок  (т.к. по условию теоремы
(т.к. по условию теоремы  ) и, значит, точки
) и, значит, точки  и С совпадают, т.е. точка О является также и серединой отрезка ВС (рис.5).
и С совпадают, т.е. точка О является также и серединой отрезка ВС (рис.5).

Доказательство достаточности. Предположим, что середина отрезка AD совпадает с серединой отрезка ВС и докажем, что
 .
.
Пусть О – середина отрезка AD; по условию О является и серединой отрезка ВС. Значит при преобразовании S симметрии относительно точки О точка А перейдет в D (рис.6), а точка В в точку С, поэтому  .
.
 Следствие. Если
Следствие. Если  , то
, то  .
.
Понятие вектора и векторное исчисление возникло в связи с рассмотрением в физике и механике Рис. 6.
таких понятий, как скорость, уско-
рение и т.д. К понятию свободного вектора мы пришли из определения равенства направленных отрезков.
Существуют и другие определения равенства двух направленных отрезков: будем говорить, что направленные отрезки  и
и  равны, если выполнены следующие условия:
равны, если выполнены следующие условия:
1) длины отрезков АВ и СD равны;
2) отрезки АВ и СD принадлежат одной прямой;
3) направленные отрезки  и
и  имеют одинаковое направление.
имеют одинаковое направление.
Тогда класс всех равных между собой направленных отрезков называют скользящим вектором.
Понятие скользящего вектора и векторное исчисление скользящих векторов возникло в механике (статике) при изучении взаимодействия сил, приложенных к твердому телу; (силу «нельзя» переносить параллельно самой себе, но можно переносить вдоль линии ее действия).
Не нашли, что искали? Воспользуйтесь поиском: