Способы задание плоскости

Рассмотрим несколько способов задания плоскости. Для этого докажем следующие теоремы.

Теорема 3.1. Через три точки, не лежащие на одной прямой, проходит плоскость и притом только одна.

Доказательство. Пусть точки А, В, С не лежат на одной прямой. По аксиоме плоскости через каждые три точки проходит плоскость. Поэтому есть плоскость, проходящая через точки А, В, С; обозначим ее 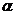. Убедимся, что она только одна.

Допустим, что через данные точки проходит еще одна плоскость , отличная от 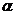. Плоскост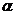и и имеют общие точки. По аксиоме 2 пересечением плоскостей является их общая прямая. Значит, эта прямая содержит все три точки общие для этих плоскостей. Но это противоречит условию теоремы, так как точки не лежат на одной прямой. Итак, через три точки проходит лишь одна плоскость.

Следствие. В пространстве существуют четыре точки, не лежащие в одной плоскости. Для каждых двух точек можно подобрать еще две точки так, что все четыре не лежат в одной плоскости.

Теорема 3.2. Через прямую и не лежащую на ней точку проходит плоскость и притом только одна.

Доказательство. Пусть даны прямая и не лежащая на ней точка А. Возьмем на прямой две точки В и С. Через три точки А, В, С, не лежащие на одной прямой, согласно теореме 1 проходит единственная плоскость. Прямая а имеет с ней две общие точки и, значит, по аксиоме 3 лежит на ней.

Теорема 3.3. Через две пересекающиеся прямые проходит плоскость и притом только одна.

Доказательство. Выберем на прямой 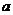точку , не являющуюся точкой пересечения прямых 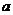и . Эта точка не лежит на прямой по построению. Проведем через прямую и точку плоскость. По теореме 2 эта плоскость существует и единственная.

Доказанные выше теоремы указывают три способа задания плоскости:

1. тремя точками, не лежащими на одной прямой;

2. прямой и не лежащей на ней точкой;

3. двумя пересекающимися прямыми.

Из доказанных утверждений вытекает, что через каждую прямую в пространстве проходит сколь угодно много плоскостей.

Не нашли, что искали? Воспользуйтесь поиском: