Перпендикуляр и наклонная. Пусть даны плоскость и не лежащая на ней точка

Пусть даны плоскость и не лежащая на ней точка. Перпендикуляром, опущенным из данной точки на данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.

Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости. Конец отрезка, лежащий в плоскости, называется основанием наклонной. Отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же точки, называется проекцией наклонной.

Наклонные и их проекции обладают следующими свойствами. Пусть из некоторой точки на плоскость проведено несколько наклонных. Тогда:

1 Любая наклонная больше как перпендикуляра, так и проекции наклонной на эту плоскость.

2 Равные наклонные имеют равные проекции и наоборот, если равны проекции, то равны и сами наклонные.

3 Большое наклонная имеет большую проекции и наоборот.

Теорема 8.1 (Теорема о трех перпендикулярах). Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной. И обратно: если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

Доказательство.

Пусть АВ – перпендикуляр к плоскости 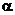, АС – наклонная и с – прямая в плоскости 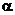, проходящая через основание С наклонной. Проведем прямую СА’, параллельную прямой АВ. По Т. 7.3 она перпендикулярна плоскости 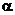. Проведем через прямые АВ и А’С плоскость . Прямая с перпендикулярна прямой СА’. Если она перпендикулярна прямой СВ, то по Т 7.1 она перпендикулярна плоскости , а значит, и прямой АС.

Аналогично если прямая с перпендикулярна наклонной СА, то она, будучи перпендикулярна и прямой СА’, перпендикулярна плоскости , а значит, и проекции наклонной СВ.

Не нашли, что искали? Воспользуйтесь поиском: