
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Критерії механічної подібності рідин, що рухаються
Незважаючи на різноманітність руху рідин у природі, можна поставити питання: яким умовам повинні відповідати параметри потоку і параметри рідин (густина, в'язкість тощо), щоб рухи рідин були механічно подібні? Якщо подібність має місце, то, знаючи картину плину рідини в одній системі, можна передбачити і характер плину рідини в іншій, геометричне подібній системі. Це має важливе значення не лише у техніці (випробування моделей літаків, кораблів тощо), айв експериментальній медицині (наприклад, при дослідженні процесів обтікання кров'ю різних моделей серцевих клапанів, особливостей плину рідин по штучних судинах, криволінійному ложеві насоса апарату штучного кровообігу тощо).
Розглядаючи будь-який плин рідин і рівняння його руху, можна виділити деякі важливі параметри рідини (η -в'язкість, ρ — густина, χ -модуль об'ємної пружності) і характеристики її руху (υ - швидкість, L - характерні розміри, τ - деякий характерний час, протягом якого відбуваються помітні зміни плину тощо). У гідродинаміці відомі декілька безрозмірних величин, що являють собою комбінацію цих параметрів. Це числа Рейнольдса (Re), Фруда (F), Маха (М), Струхаля (S). Кожне з цих чисел має певний фізичний зміст. Так, число Маха є відношенням швидкостей руху тіла і звука у даному середовищі (М= υ/c). Число Струхаля - відношення деякого характерного розміру потоку рідини і розмірів тіла (S = υ*τ/L). Число Фруда (Ф = υ2lgL) визначає відношення кінетичної енергії рідин до її приросту, обумовленого роботою сили тяжіння на деякій характерній відстані (чим більше число Фруда, тим більша роль інерції у порівнянні з дією сили тяжіння).
Одним з найважливіших критеріїв подібності є число Рейнольдса. За порядком величини воно дорівнює відношенню кінетичної енергії рідини до витрати її, обумовленої роботою сил в'язкого тертя на характерній довжині. Дійсно, кінетична енергія рідини Ек ~ ρL3υ2, робота сил в'язкості А = = Fm*L. Силу в'язкого тертя знайдемо за
формулою Ньютона Fm ~  . Відношення кінетичної енергії Ек до роботи А і становить число Рейнольдса:
. Відношення кінетичної енергії Ек до роботи А і становить число Рейнольдса:
 (1.30)
(1.30)
Число Рейнольдса, таким чином, визначає відносну роль інерції і в'язкості рідини при її плині. При великих числах Рейнольдса головну роль відіграє інерція, при малих - в'язкість. При плині рідини по циліндричних трубках у ролі характерного розміру L часто використовують радіус чи діаметр судини. Потоки рідин вважаються подібними, якщо для них числа Рейнольдса і Фруда збігаються. При малих числах Рейнольдса плин в'язких рідин є ламінарним, при зростанні швидкості ламінарний плин стає нестійким і перетворюється в турбулентний. Турбулентний плин - це такий плин, гідродинамічні характеристики якого (швидкість, тиск) різко та нерегулярно змінюються з часом і у просторі. Частинки рідини рухаються по складних траєкторіях, рідина інтенсивно перемішується. Прикладом такого
руху є рух крові при її вигнанні з шлуночків серця, її плині по аорті тощо.
Слід зауважити, що при турбулентному русі рідини не діють звичайні формули гідродинаміки (гемодинаміки). Так, на відміну від закону Гагена-Пуазейля і формули Пуазейля, згідно з якими при ламінарному плині об'ємна швидкість Q чи лінійна швидкість v пропорційні різниці тисків υ ~ ~ Р1- Р2 У першому степені, при турбулентній течії рідини за певними умовами має місце закон Шезі, згідно з яким лінійна швидкість υ~  . Для рідини, що тече по певній судині, можна визначити значення швидкості υкp, при якій рух із ламінарного перетворюється у турбулентний. Число Рейнольдса, при якому відбувається це явище, зветься критичним:
. Для рідини, що тече по певній судині, можна визначити значення швидкості υкp, при якій рух із ламінарного перетворюється у турбулентний. Число Рейнольдса, при якому відбувається це явище, зветься критичним:
 . (1.31)
. (1.31)
У геометричне подібних системах перехід від ламінарного до турбулентного плину відбувається завжди при одних і тих самих значеннях числа Рейнольдса. Так, згідно (1.31) критичне значення числа Re для в'язкої рідини, що тече по довгій циліндричній трубці, становить 2300. Значення чисел Рейнольдса для крові в різних ділянках судинного русла подані у табл. 1.2.
Зауважимо, що зміна величини в'язкості крові (наприклад, при анемії) може діагностуватися завдяки виникненню турбулентних шумів. Це пояснюється тим фактом, що при анемії коефіцієнт в'язкості зменшується у 2-3 і більше разів. Відповідно число Рейнольдса збільшується, оскільки Re ~ 1/η\. Як наслідок, число Рейнольдса стає більшим за своє критичне значення і виникає перехід від ламінарного плину крові до турбулентного.
Ще одне медичне застосування переходу між ламінарною і турбулентною течією крові пов'язане з вимірюванням кров'яного тиску методом Короткова. У цьому методі систолічний (верхній) тиск вимірюється у момент, коли кров починає протискуватися через отвір в артерії, стиснутій за допомогою манжети. Саме у цей момент виникають шуми, обумовлені появою турбулентної течії крові. Діастолічний (нижній) тиск фіксується у момент, коли ці шуми зникають внаслідок послаблення манжети і переходу течії від ламінарної до турбулентної.
Пульсові хвилі
Існування пульсових хвиль легко виявити. Для цього достатньо притиснути пальцем променеву або сонну артерії і відчути "биття" стінки артеріальної судини. Чутливі пристрої можуть зареєструвати коливання стінок і венозних судин, які значно слабкіші за коливання артеріальних судин. Як виникають пульсові коливання, у чому полягає їх фізична природа? Проблема ця досить складна і вирішена лише частково. Плин крові по судинному руслу супроводжується різноманітними коливаннями: це і поздовжні хвилі тиску, що поширюються у рідкому середовищі зі швидкістю звуку, це і періодичні зміни швидкості руху рідини, пов'язані з переривчастим викидом крові серцем в судинне русло, це і періодична зміна просвіту судини при зміні його кровонаповнення. Всі ці процеси взаємопов'язані, вони характеризують єдине явище - рух крові по складному дереву судинного русла.
Розглянемо спрощену модель виникнення пульсових хвиль в еластичній судині. Зрозуміло, що їх походження пов'язане з діяльністю серця. Коли б на виході серця плин крові був сталим, то ніяких пульсацій не виникало б. З іншого боку, коли б стінки судин були дуже жорсткими, то навіть при пульсуючому кровотоці рух стінок був би практично непомітним. Отже, походження пульсових хвиль пов'язане з реакцією пружних стінок судини на пульсуючий плин крові, що виникає при періодичній роботі серця.
Виділимо невелику ділянку еластичної судини (мал. 1.19), на одному з кінців якого знаходиться поршень. На
поршень короткочасно діє сила F. Рідина біля поршня внаслідок її інерції не встигає переміститися вздовж судини, дія сили викликає зростання тиску на стінки -ділянка розширюється доти, доки напруження стінки не компенсує зростання тиску всередині судини. Оскільки натяг стінки у цій області буде більшим, ніж у сусідніх, рідина буде переміщуватися далі по судині. Переміщення рідини приведе до зменшення тиску на цій ділянці, судина почне відновлювати первісний об'єм у той час, як об'єм сусідньої ділянки буде зростати. Процес повторюється після нового поштовху поршня. По еластичній стінці буде поширюватися пульсова хвиля.

Мал. 1.19. Модель ділянки еластичної судини.
Запишемо рівняння пульсової хвилі. Для цього розглянемо рух ідеальної рідини по еластичній трубці під дією одних лише сил тиску. Виділимо ділянку завдовжки Ах і об'ємом V. Позначимо зміну радіуса ділянки трубки при розширенні через £, тоді поточне значення радіуса дорівнюватиме
R(x,t) = R0 + e(x,t). (1.32)
Рівняння пульсової хвилі, яке характеризує процес розповсюдження зміни радіуса судини є вздовж її осі, має такий вигляд:
 , (1.33)
, (1.33)
де и  — - швидкість поширення пульсової хвилі.
— - швидкість поширення пульсової хвилі.
За умови відсутності поздовжнього натягу (так, що трубка буде скорочуватись при розширенні) модуль об'ємної пружності χ для тонкої циліндричної судини радіусом R і товщиною стінки h визначається за формулою (1.7) без множника 1 - μ 2. Після підстановки маємо формулу Моєнса-Кортевега для швидкості:
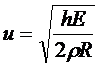 (1.34)
(1.34)
Таким чином, швидкість поширення пульсової хвилі залежить як від геометричних параметрів судини (радіуса і товщини), так і від пружних властивостей судинної стінки.
Коефіцієнт Пуассона для судини є величина постійна і дорівнює приблизно 0.5. Модуль Юнга, як було показано вище, не залишається величиною сталою для судини, тому швидкість поширення пульсових хвиль може значно змінюватися. Деякі приклади зміни швидкостей розповсюдження пульсових хвиль наведено на мал. 1.20. Швидкість пульсової хвилі значно змінюється при різних судинних захворюваннях, у зв'язку з цим її клінічне визначення дозволяє одержати додаткову інформацію для оцінки функціонального стану стінок судин.

Мал. 1.20. а) зміна швидкості з ростом тиску (1, 2, 3 - відповідно для похилого, середнього та молодого віку), б) зміна швидкості з
віком.
Рух крові по серцево-судинній системі досить складне явище. Складну будову має кровоносне русло, що являє собою розгалужену систему еластичних судин різного типу. Сама рідина - кров - є складна суспензія, реологічні характеристики якої залежать від умов її плину. Система кровообігу має активні джерела енергії (шлуночки і передсердя серця). Різні активні фізіологічні процеси (механізми рефлекторної зміни тонусу судин та продуктивність серця) змінюють фізіологічні властивості системи кровообігу, а отже й умови руху крові. Будь-який опис процесів гемоди-наміки (від простих випадків механіки руху крові до складних процесів рефлекторного керування кровообігом) базуються на експериментальних даних, накопичених за багато років досліджень. У таблиці 1.2 наведено деякі показники системи кровообігу в стані спокою і при навантаженні.
Таблиця 1.2. Деякі показники системи кровообігу людини в нормі і при навантаженнях
| № | Параметри системи кровообігу | Значення |
| 1. | Середня лінійна швидкість в аорті - в капілярі - у вені | 0.3-0.4, м/с 0.002-0.01 м/с 0.2-0.4 м/с |
| 2. | Середній артеріальний тиск - спокій - максимальне навантаження | 90- 100 мм рт. cm. вище за 200 мм рт. cm. |
| 3. | Середній тиск у капілярах | 25-30 мм рт. cm. |
| 4. | Хвилинний об'єм крові - спокій - максимальне навантаження | 5-6 л/хв. Вище за 20 л/хв. |
| 5. | Швидкість пульсової хвилі (артерія) | 4-6 м/с |
| 6. | Число Рейнольдса в аорті у вені в капілярі | 3000-4000 500-700 0.001 |
| 7. | Площа перерізу - аорти - капілярів | = 3 см2 = 1200c.w2 |
Не нашли, что искали? Воспользуйтесь поиском: