Затухаючі коливання і аперіодичний рух

Припустимо, що в розглянутих системах існує тертя чи опір, причому сила тертя (опору) пропорційна швидкості: F_m=-rυ, де r - коефіцієнт тертя (опору). Запишемо в цьому випадку рівняння руху (II закон Ньютона).

ma = -kx-rυ або .

Позначивши ,отримаємо диференційне рівняння другого порядку, що описує рух пружинного маят­ника у присутності сил тертя

. (1.49)

Складемо характеристичне рівняння, що відповідає ди-ференційному рівнянню (1.49):

.

Знайдемо корені характеристичного рівняння

. (1.50)

Загальний розв'язок рівняння (1.49) залежить від знака різниці β²-ω₀². Розглянемо всі можливі випадки:

1. β²<ω₀², коли корені характеристичного рівняння є комплексними числами (затухаючі коливання)

,

де - циклічна частота. У випадку комплекс­них коренів характеристичного рівняння загальний розв'я­зок (1.49) має вигляд

, або

, (1.51)

де A(t) = A₀e ^-βt- амплітуда коливань, яка зменшується за експоненціальним законом, (β - коефіцієнт затухання, визначає швидкість затухання амплітуди. Залежність х = f (t) для затухаючих коливань подано на мал. 1.23.

Мал. 1.23. Затухаючі коливання.

Ступінь затухання часто характеризують декрементом затухання S і логарифмічним декрементом затухання λ*:

,

де період затухаючих коливань дорівнює

2. β²>ω₀², коли корені характеристичного рівняння є дійсними числами (аперіодичні коливання)

<0

У цьому випадку загальний розв'язок рівняння (1.49) ма­тиме вигляд

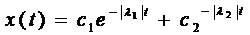(1.52)

що відповідає аперіодичному рухові (мал. 1.24).

3. β²>ω₀², коли корені є кратними. Легко побачити, що і в цьому випадку рух тіла буде аперіодичним.

Коливання, що виника­ють у системі при відсут­ності зовнішніх сил, нази­вають вільними. Частота вільних коливань залежить як від пружних власти­востей системи (ω₀), так і від інтенсивності втрат (β). Якщо β²<<ω₀², то ω ω₀ i період вільних коливань

стає близьким до періоду власних коливань (мал. 1.23).

Мал. 1.24. Аперіодичний рух.

Вимушені коливання

Припустимо, що на матеріальну точку масою m, крім пружної або квазіпружної сили і сили тертя, діє зовнішня вимушуюча сила, що змінюється за періодичним законом

F₃ = F₀sin Ωt,

де F₀ - амплітуда, а Ω - циклічна частота вимушуючої сили. В цьому випадку рівняння руху матиме вигляд

ma = - kx - r + F₀sinΩlt, або

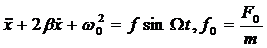. (1.53)

Загальний розв'язок диференційного рівняння (1.53) має вигляд

х = Asin(Ωt + φ₀), (1.54)

де А - амплітуда вимушених коливань, яка дорівнює

, (1.55)

а початкову фазу φ₀ визначають з рівності:

. (1.56)

Важливу формулу (1.55) для амплітуди А вимушених коливань можна отримати, скориставшись графічним мето­дом розв'язку неоднорідних диференційних рівнянь 2-го порядку з постійними коефіцієнтами. З формули (1.54) для зміщення х легко отримати вирази для похідних

Якщо намалювати "векторну" або "фазову" діаграму (мал. 1.25а), відклавши на ній амплітудні значення всіх доданків у рівнянні (1.53) з урахуванням зсуву їх фаз, то очевидно, що векторна сума трьох доданків у лівій частині (1.53) повинна дорівнювати амплітудному значенню виму­шуючої сили, тобто . Звідси безпосередньо випливає формула (1.55) для амплітуди А, так само як і формула (1.56) для tgφ.

Мал. 1.25а. Векторна діаграма для визначення амплітуди А і початкової фази φ₀.

Таким чином, якщо на тіло, яке коливається, діє зовнішня періодична сила з частотою Ω, то тіло здійснює коливання з тією ж частотою, причому амплітуда коливань залежить від амплітуди і частоти зовнішньої сили, від коефіцієнта затухання, від пружних властивостей системи і маси тіла, яке коливається. Такі коливання називають вимушеними.

Не нашли, что искали? Воспользуйтесь поиском: