Включение индуктивности на синусоидальное напряжение

Если в схеме (см. рис.1.2) источник постоянной э.д.с. заменить источником синусоидальной э.д.с. (e = E_msin(w t + y), то можно записать аналогичное уравнение:

. (1.20)

Это неоднородное уравнение первого прядка с тем же характеристическим уравнением с соответствующим корнем. Поэтому решение полученного уравнения можно записать по аналогии:

i = i_пр + Ae^{a t} . (1.21)

Однако определение принужденного режима и постоянной интегрирования несколько отличается. Принужденное значение рассчитывается так же как в цепи переменного синусоидального тока. В комплексной форме можно записать:

. (1.22)

В синусоидальной форме

i_пр =I_{пр m} sin(w t +y – φ) . (1.23)

При t = 0 i (0) = 0. Поэтому

0 = I_{пр m} sin(y – φ) + Ae^{ja 0} , (1.24)

A = – I_{пр m} sin(y – φ) . (1.25)

Окончательно, закон изменения тока будет иметь следующий вид:

i = I_{пр m} sin(w t +y – φ) – I_{пр m} sin(y – φ) e^{ja t} . (1.26)

Напряжение на индуктивности равно

. (1.27)

Правильность полученных выражений можно проверить, вычислив значения тока и напряжения в начальный момент времени, и сравнив полученные значения с начальными условиями. При t = 0 выражение для тока дает ноль, выражение для напряжения после некоторых преобразований дает u_L(0) = U_msin y . Так как в момент включения ток равен нулю, все напряжение источника прикладывается к индуктивности. Кривая тока вместе с составляющими приведена на рис.1.6, а. Она показывает, что по мере затухания свободной составляющей переходный ток стремится к своему установившемуся значению. Однако в начале переходного процесса амплитуда тока превышает амплитуду установившегося значения, что зачастую приводит к ложным срабатываниям релейной защиты. Здесь возможны два крайних случая – свободная составляющая равна нулю, и свободная составляющая максимальна.

Переходный процесс отсутствует, если свободная составляющая равна нулю. При этом sin (y - j) = 0, из чего следует, что y = j. Это значит, качество переходного процесса зависит от момента коммутации. Если включить рубильник в момент перехода ожидаемого тока через ноль, то переходного процесса не будет.

Если sin (y - j) = 1, то свободная составляющая максимальна (рис.1.6, в).

1.6. Включение цепи R, L, C на постоянное напряжение

Рассмотрим схему (рис. 1.7). Здесь имеется два накопителя энергии – индуктивность и емкость. Составим уравнение по второму закону Кирхгофа для послекоммутационной цепи:

iR + и_а + и_а = Е . (1.28)

Имея в виду, что

, и , ,

получаем

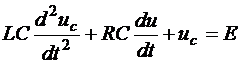, (1.29)

или

. (1.30)

Это есть дифференциальное уравнение второго порядка относительно напряжения на конденсаторе с правой частью. Решение этого уравнения так же состоит из принужденной и свободной составляющей:

u_c = u_cпр + u_cсв .

Принужденная составляющая может быть найдена из дифференциального уравнения путем приравнивая нулю производных. Таким образом, получаем

u_cпр = Е.

Свободная составляющая определяется из дифференциального уравнения без правой части в виде :

, (1.31)

где А₁ , А₂ – постоянные интегрирования;

a₁, a₂ – корни характеристического уравнения.

Запишем характеристическое уравнение:

. (1.32)

Введем обозначения: , . Тогда

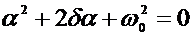, (1.33)

откуда .

Возможны три случая при нахождении корней характеристического уравнения:

1) , тогда корни будут вещественны, отрицательны и различны;

2) , тогда корни будут вещественны, отрицательны и одинаковы;

3) 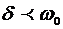, корни сопряжено комплексные с отрицательной вещественной частью.

В первом случае будет апериодический переходный процесс, в третьем –

колебательный. Второй случай характеризует граничный режим, т.е. лежит между апериодическим и колебательным процессом.

Рассмотрим апериодический процесс, при котором корни вещественные, отрицательные и разные. Тогда

. (1.34)

Постоянные интегрирования определяются с учетом начальных условий. Здесь требуется два начальных условия, так как в уравнении два неизвестных А₁ и А₂. Одно начальное условие определяется по закону коммутации и называется основным. Напряжение на конденсаторе перед коммутацией было равно нулю:

.

Ток в индуктивности равен нулю, так как цепь была разомкнута:

i_L (0) = 0.

Для определения двух постоянных интегрирования нужно еще одно уравнение. Возьмем производную от первого уравнения:

. (1.35)

Определим значение производной в первый момент времени после коммутации по зависимости тока и напряжения на конденсаторе . Ток в емкости равен току в индуктивности, поэтому

.

Запишем уравнения (1.34), (1.35) для момента времени t=0 :

Решение этой системы имеет вид:

, (1.36)

. (1.37)

Подставим полученные значения постоянных в уравнение (1.34) и после небольших преобразований получим:

. (1.38)

Или

. (1.39)

Последнее выражение показывает, что закон изменения напряжения на конденсаторе после коммутации состоит из постоянной составляющей и двух экспоненциальных функций с постоянными времени

.

Ток в емкости определяется через производную:

. (1.40)

По теореме Виета

.

Тогда

, (1.41)

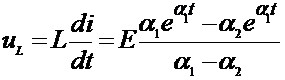. (1.42)

1.7. Построение графиков зависимостей

Определим значения функций в крайних точках.

t = 0

i (0) = 0

u_c (0) = 0

u_L (0) = E

t = ∞

i _пр = 0

u_{c пр} = Е

u_{L пр} = 0

Кривая тока в начальный момент и в конце процесса равен нулю. При этом в начале процесса производная тока не равна нулю, так как

.

В середине процесса ток имеет максимум, совпадающий с переходом напряжения на индуктивности через нуль (t = t₁).

Скорость изменения напряжения на конденсаторе в начале процесса равна нулю

.

Это значит, кривая изменения напряжения на конденсаторе имеет точку перегиба в точке перехода напряжения на индуктивности через нуль, так как в этой точке

В интервале времени до t₁ ток возрастает, а индуктивность препятствует этому и напряжение на нем имеет положительное направление. После этого момента ток начинает уменьшаться и напряжение на индуктивности меняет свой знак. Отрицательный максимум напряжения совпадает с точкой перегиба кривой тока (t = t₂)

.

Кривые изменений тока, напряжения на емкости и индуктивности изображены на рис. 1.8 .

Рис. 1.8

Рассмотрим случай колебательного процесса. Здесь , или

и . (1.43)

Преобразуем выражение для корней:

.

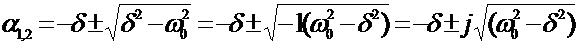Введем обозначение . Тогда

Для нахождения законов изменения при комплексно сопряженных корнях необходимо обратится к формулам Эйлера:

Из этих формул вытекает следующее:

, .

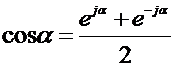Преобразуем выражение для тока с использованием формулы Эйлера:

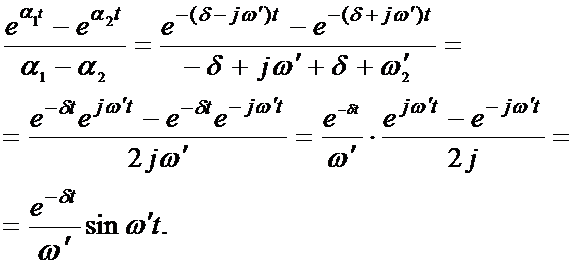
Итак

. (1.46)

Аналогичным способом можно определить другие законы изменения. Имеется всего три конструкции, которые дают формулы перехода к колебательным функциям.

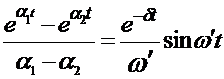, (1.47)

, (1.48)

, (1.49)

где ;

;

С учетом изложенного выше, можно записать окончательно:

, (1.50)

, (1.51)

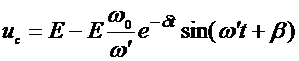. (1.52)

Это затухающие синусоиды, графическое изображение которых приведено на рис. 1.9.

Рис. 1.9

В зависимости от параметров цепей синусоиды могут быть различными (рис. 1.10, а. б ) Такие затухающие синусоиды характеризуют с помощью декремента колебания. Декремент – отношение двух соседних максимумов кривой (см. рис. 1.9).

а)

б )

Рис. 1.10

. (1.53)

Но , тогда

. (1.54)

Величина называется логарифмическим декрементом колебания

Не нашли, что искали? Воспользуйтесь поиском: