Правила дифференцирования и интегрирования

Пусть имеется функция и его изображение . Возьмем производную от оригинала:

. (2.9)

Это новая функция времени. Определим ее изображение по преобразованию Лапласа.

. (2.10)

Воспользуемся методом интегрирования по частям:

.

Введем обозначения

. (2.11)

Здесь второе слагаемое есть изображение оригинала, умноженное на оператор p, первое слагаемое раскрывается следующим образом. При подстановке верхнего предела первый сомножитель стремится к нулю. Второй сомножитель может стремиться к бесконечности. Однако все электротехнические функции стремятся к бесконечности медленнее, чем первый сомножитель к нулю. Поэтому произведение равно нулю.

Подстановка нижнего предела дает начальное условие. Таким образом

. (2.12)

Окончательно:

.

Если начальные условия нулевые, т.е. – f (0) = 0, то

.

Отсюда следует, что дифференцированию оригинала соответствует умножению изображения на оператор р.

2. Пусть функция имеет изображение: f (t) == F (p). Возьмем интеграл от оригинала

. (2.13)

Применим преобразование Лапласа к данной функции

. (2.14)

Этот интеграл можно взять так же по частям. Но если t= 0, то ψ (0) = 0. Тогда

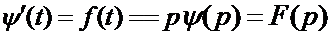, (2.15)

. (2.16)

Интегрированию оригинала соответствует делению изображения функции на оператор р.

Не нашли, что искали? Воспользуйтесь поиском: