
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Жылу двигателi. Карно циклi 1 страница
Билет.
Сұйықтар. Беттік керілу. Беттік керілу коэффициенті. Лаплас формуласы. Капиллярлық құбылыстар.
Сұйық деп – көлемін өзгертпейтін, механикалық әсерлесулердің тарапынан пішінін тез өзгертуге бейім заттың агрегаттық күйінің бір түрін айтады. Фаза деп шекаралық бетпен бөлінген, барлық нүктелерде физикалық қасиеттері бірдей жүйе бөлігі айтылады. Беттік керілу — екі фазаның (дененің) бөліну бетінің термодинамикалық сипаттамасы. Өлшем бірліктері Дж/м2 немесе Н/м. Беттік керілуді бөліну беті сұйықтық болған жағдайда, бет контурының ұзындық бірлігіне әсер ететін және фазалардың берілген көлемдерінде бетті ең кіші шамаға (минимумға) дейін жиыруға ұмтылатын күш ретінде де қарастыруға болады. Екі қоюланған (конденсацияланған) фазаның шекарасындағы беттік керілу, әдетте, фазааралық керілу деп аталады. Сұйықтың табиғатына қарай анықталатын пропорционалдық коэффициент σ – беттік керілу коэффициенті д.а. Ол сан мәні жағынан бір өлшем ұзындыққа сәйкес келетін беттің керілу күшіне тең, яғни 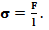
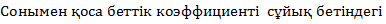 қабыршақтың ауданын бірлік өлшемге кемітуге жұмсалатын жұмыс. σ=ΔA/ΔS. Процесс тұрақты температурада жүреді, сондықтан беттің керілу коэффициенті өзгермейді, ал қабыршақты созатын сыртқы күштің жасаған жұмысы ΔA оның потенциалдық энергиясын ΔE-ге арттырады, яғни ΔE=-ΔA, бұл энергия сұйықтың еркін бетінің энергиясы деп аталады, сонда σ=ΔE/ΔS. Бұл сұйықтықтың беттік керілу коэффициенті, бірлік ауданына келетін еркін бет энергиясы деп анықталады. Қысым бір дене екінші дене бетіне (мысалы, ғимарат іргетасының грунтқа, сұйықтықтың ыдыс қабырғасына,газдың піспекке, т.б.) әсер еткенде пайда болатын қалыпты күштің (дене бетіне перпендикуляр) қарқындылығын сипаттайтын физикалық шама. Капиллярлық қысым — судың капиллярлық көтерілу биіктігіне сәйкес келетін қысым. Мұндай қысым жайында заңдылықты теория жүзінде алғаш дәлелдеген белгілі француз ғалымы П. Лаплас (1806 жылы).
қабыршақтың ауданын бірлік өлшемге кемітуге жұмсалатын жұмыс. σ=ΔA/ΔS. Процесс тұрақты температурада жүреді, сондықтан беттің керілу коэффициенті өзгермейді, ал қабыршақты созатын сыртқы күштің жасаған жұмысы ΔA оның потенциалдық энергиясын ΔE-ге арттырады, яғни ΔE=-ΔA, бұл энергия сұйықтың еркін бетінің энергиясы деп аталады, сонда σ=ΔE/ΔS. Бұл сұйықтықтың беттік керілу коэффициенті, бірлік ауданына келетін еркін бет энергиясы деп анықталады. Қысым бір дене екінші дене бетіне (мысалы, ғимарат іргетасының грунтқа, сұйықтықтың ыдыс қабырғасына,газдың піспекке, т.б.) әсер еткенде пайда болатын қалыпты күштің (дене бетіне перпендикуляр) қарқындылығын сипаттайтын физикалық шама. Капиллярлық қысым — судың капиллярлық көтерілу биіктігіне сәйкес келетін қысым. Мұндай қысым жайында заңдылықты теория жүзінде алғаш дәлелдеген белгілі француз ғалымы П. Лаплас (1806 жылы). 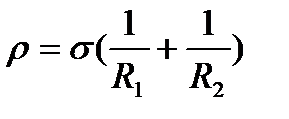
Мұнда p – сұйықтықтың сығылған бетіндегі қысым, σ – беттік керілу,  - сұйық бетінің ағысына перпендикуляр екі қисықтың радиусы
- сұйық бетінің ағысына перпендикуляр екі қисықтың радиусы
Лаплас түрлендіруі — “оригинал” деп аталатын түрлендіру. Лаплас түрлендіруі операциялық есептеулерде, автоматты реттеуіштерге байланысты есептерді шешкенде жиі қолданылады. Электротехника, гидродинамика, жылу өткізгіштік, механика есептерінің бірқатары Лаплас түрлендіруі қолданалатын әдістер арқылы шешіледі.
Билет.
Нақты газдар. Ван-дер-Ваальс теңдеуі. Ван-дер-Ваальс изотермалары. Эндрюстің эксперименттік изотермалары. Газ-сұйық фазалық ауысуы
Нақты газдар
Табиғаттағы құбылыстарды зерттеу барысында, ғалымдар тәжірбиелік мәндерге сүйене отырып, осы құбылыстарды сипаттайтын физикалық шамалардың арасындағы мөлшерлік байланыстарды тағайындады. Бірақ көп жағдайда, бұл қатынастар, заңдар мен оған кіретін шамалардың мәндері белгілі бір шектерде табылғанда ғана дұрыс. Яғни, барлық заңдардың қолданылу шегі болады.
Сондықтан, нақты газдарда молекулалардың әсерлесу күштерін, олардың көлемдерін ескермей кетуге болмайды. Мысалы, әр түрлі қысымдағы және 273К температурадағы бір моль азот үшін Бойль-Мариотт заңының орындалмайды.
Газ қысымын 1000 атмосфераға көтергенде Бойль-Мариотт заңынан ауытқу 2-еседен асатыны көрінеді. Мұндай ауытқулар, молекулалардың ара қашықтығы, олардың сызықтық өлшеммен шамалас болған кезде де байқалады. Мысалы, азот молекуласының көлемі 
Ал бір моль газда 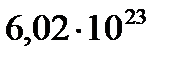 1/моль молекула бар екендігін ескерсек, олардың көлемі
1/моль молекула бар екендігін ескерсек, олардың көлемі  екендігі шығады. Яғни, бір моль газдың көлемін
екендігі шығады. Яғни, бір моль газдың көлемін 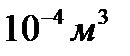 мәнге әкелсе, олардың идеалдықтан ауытқуы үлкен мәндерге жетеді және осы үшін бұрынғы тағайындалған заңдар орындалмайды.
мәнге әкелсе, олардың идеалдықтан ауытқуы үлкен мәндерге жетеді және осы үшін бұрынғы тағайындалған заңдар орындалмайды.
Ван-дер-Ваальс
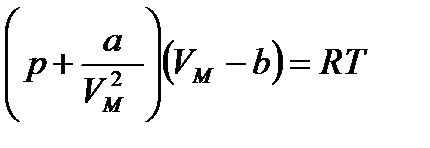 Ван-дер-Ваальстың теңдеуін жақшаларын ашып, қарапайым түрлендіруден кейін мына түрге келтіруге болады:
Ван-дер-Ваальстың теңдеуін жақшаларын ашып, қарапайым түрлендіруден кейін мына түрге келтіруге болады:

Екі жағын p-ға бөліп, бұл теңдеуді былай жазамыз:
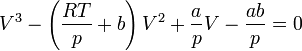

V көлемге қатысты осы теңдеу үшінші дәрежелі, сондықтан оның 3 түбірі болады: 3 нақты немесе 1 нақты екі жорамал түбірі бар. Демек бір қысымның мәніне көлемнің әр түрлі 3 мәні сәкес келеді. Ван-дер-Ваальс теңдеуінің түбірлерінің мағынасын ашу үшін
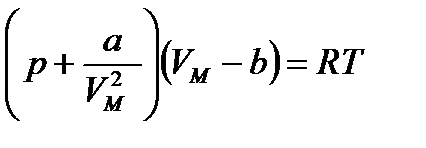
бойынша изотермдерін,яғни тұрақты температурада қысымның көлемге қатысты тәуелділігін талдау қажет, онда
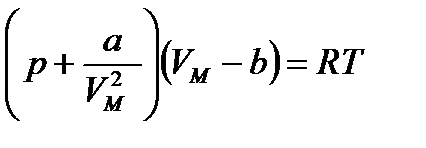
мына түрде жазу қолайлы:
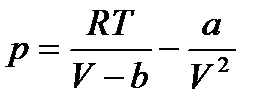
Осы теңдеу бойынша теориялық изотермнің минимумдары, максимумдары бар, V=b болғанда, p=∞ екенін байқаймыз.Сондықтан V-көлем b-дан кем болуы мүмкін емес олай болса газ орналасқан ыдыстың көлемі барлық молекулалардың төрт еселенген көлемінен болуы мүмкін емес Ван-дер Ваальс теңдеуі б-ша СО2 үшін әртүрлі есептелген теориалық суретте көрсетілген.
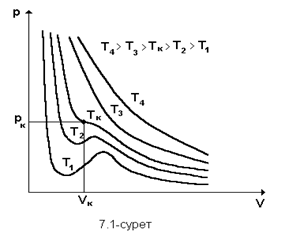
Ван-дер Ваальс изотерімдердің түрі идеал газдікіндей гипербола болмайтыны осы графиктен айқын көрінеді. Температура өскен сайын суреттегі теориялық изотермдердің ерекше толқын тәріздес иіліс бөлімі кішірейіп, Т=Тк деп белгіленген изотермнің нүктесінде жойылады. Осы Тк температурасы критикалық температура д.а. Температуралары Т>Тк критикалықтан жоғары изотермдер үзіліссіз бірсарынды өзгеретін қисықтар, түрлері гипербола сияқты идеал газдікіндей болады. Температуралары Т<Тк критикалықтан төменгі изотермдердің орта бөлімдерінде ерекше толқын тәріздес иіліс болады. Ван – дер – Ваальс тің теориялық изотермінің 7.1 сурет тәжірибе бойынша анықталған нақты газ изотермімен 7.2 суретті салыстырайық. Бұл изотермдердің газ тәріздес күй аймығы – ab бөлігі, сұйық күй аймағы – fg бөлігі, бір – бірімен үйлеселді. Бірақ, осы изотердерде негізгі ерекшеліктері бар; ол эксперементтік изотермдегі bdf және теориялық изотерміндегі cde бөлімдерімен байл. сde нүктелеріне сәйкес күйлер табиғатта болмайды. Себебі, көлемнің қысымға тәуелділігі әдеттен тыс, онда қысым өскенде, көлем кішіреймейді, олда ұлғаяды. Табиғатта қысымы өскенде өзінің көлемін ұлғайтатын, демек тығыздығын кемітетін заттар кездеспейді. Тіпті осындай ғажайып қасиетке ие заттар болса да, олардың күйлері өте орнықсыз болуы керек. Осы cde бөліміне сәйкес күйлерді орнықсыз немесе стабильді емес д.а. Vc және Vе көлемнің мәндері үшін 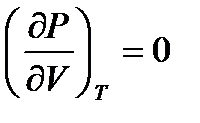 , ал осы көлемдер аралығында бұл туынды оң таңбалы. P=const сызыгы (fdb) изотермдері үш нүктеде қиып өтеді 7.1 сурет, демек қысымның бір мәніне көлемнің 5.25тің үш түбірі сәйкес келеді Т =const. Осы қысымға сәйкес Vf және Vbгаз тәріздес фазаларының көлемдері болады. Көлемнің үшінші Vd мәні
, ал осы көлемдер аралығында бұл туынды оң таңбалы. P=const сызыгы (fdb) изотермдері үш нүктеде қиып өтеді 7.1 сурет, демек қысымның бір мәніне көлемнің 5.25тің үш түбірі сәйкес келеді Т =const. Осы қысымға сәйкес Vf және Vbгаз тәріздес фазаларының көлемдері болады. Көлемнің үшінші Vd мәні 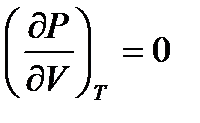 оң таңбалы болатын изотермнің сde бөліміне жатады. Осы с мен е аралығындағы кез күйлер орнықсыз (стабильді емес) болады bс және еf аралығындағы күйлер метастабильді д. а, олар заттың біртекті тұрақсыздау күйлерін анықтайды.
оң таңбалы болатын изотермнің сde бөліміне жатады. Осы с мен е аралығындағы кез күйлер орнықсыз (стабильді емес) болады bс және еf аралығындағы күйлер метастабильді д. а, олар заттың біртекті тұрақсыздау күйлерін анықтайды.
Теориалық изотерімнің ab газ тәріздес күйіне, fg сұйық күйіне, сde заттың сұйығы мен буының тепе-теңдік күйде болатын, демек екі фазалық күйіне сәйкес келеді. тәжірибеден анықталған изотерімнің bdf бөлімінде көлем өзгергенімен қысымы өзгермейді. Оның себебі, көлем кішірейгенде будың бір бөлігі сұйыққа айналады (КОНДЕНЦАЦИЯЛАНАДЫ) қысым өзгермейді сол мәнде қалады. Керісінше көлем ұлғайғанда, сқйықтың бір бөлігі буланады да қысым сол қалыпта қалады.
Изотерманың fg сұйық күйге сәйкес. Мында көлем аз ғана өзгергенде қысым елеулі өседі, себебі сұйықтын сығылуы өте аз. Заттың bc бөлігіне сәйкес күйлері газ тәріздес, бірақ бұл газдың қысымы сол температурадағы қаннықан будың өысымынаң артық, демек табиғилыққа қарсыкеледі. Заттың мұндай ерекше күйі жабық ыдыстағы ылғал ауанны өте тез суытқанда байқалады. Мұндай буды аса қаныққан бу д.а.
Бқл күй өте орнықсыз мұны оны көбінесе метастабильді күй дейді. Аса қаныққан буды алу үшін канденцация орталықтарын жою керек. Аса қанықан буды конденцация центірлері пайда болғанда будың артық мөлшері сұйыққа айналады, бу қанығады изотерманын bc бөлігіндегі күйлер bdf бөлігіндегі нүктелерге ауысады.
fe бөлігіндегі сұйықтың қысымы қанныққан будың қысымынаң кіші болады. Бұл күй де метастабильді, орнықсыз. Булану орталықғы пайда болысымен, сұйық қатты қайнайды, сұйық үстіндегі будың қысымы көбейедіде, изотермның fe бөлігіндегі күйлерге көшеді. Қысымы қаннықан бу қысымынаң төмен сұйықты аса қыздырылқан дейді.

Газ-сұйық фазалық ауысуы
Заттың бірқатар физикалық қасиеттерінің бір-біріне ауысуын секірмелі түрде өтуі, мысалы судың буға айналуы н-cе будың суға айналуы, мұздың еруі заттың агрегаттық күйлері д.а.
Ван-дер-Ваальстың изотермдерің Максвелдің тандауы б-ша fedf және dcbd аудандары бірдей болатындай, bdf түзу сызығы бойымен зат f күйден b күйге өтеді. Онда зат бір фазалық fedcb қыйсығымен, әлде екі фазалық bdf түзуімен өтеме істелінетін жұмыс бірдей. Сурет онда fedcb қыйсығымен шектелетін аудан bdf түзуінің астындағы ауданға тең болады. Сондықтаң fedcb қыйсығының өркештерінің аудандары тең болады.
Ван-дер-Ваальс теңдеуі заттың екі фазасын: газ тәріздес (ab бөлігі) және сұйық (fg бөлігі) бейнеленгенімен одан түзу сызықты bdf бөлігінің орны аңықталмайды.
Ван-дер-Ваальс теңдеуін тәжірибе арқылы тексергенде, оның нақты газдардың p,v,t параметірлер арасындағы қатынастар жуықтап қана суреттейтіні көрінді. Теңдеудің a ж.е b тұрақтылары да температурақа тәуелді болып шықты. Сол себептен Ван-дер-Ваальс теңдеуі нақты газ күйін жуықтап қана бейнелейді. Ван-дер-Ваальс теңдеуінен тікелей шығатың өте маңызды мәселе-заттың критикалық температурасы мен критикалық күйінің болуы.
Эндрюс тәжірибесі
Ван-дер-Ваальс изотермалары тәртібінің физикалық мағынасын анықтау үшін ағылшын химигі Эндрюстің 1869ж. қойған тәжірибесінің нәтижелерін пайдаланған жөн. Эндрюс көмірқышқыл газдың изотермаларын зерттеген.
Тәжірибелік изотермалардың горизонталь аймақтары тұрақты қысымда өтетін газдың сұйық күйге айналу кезеңіне сәйкес келеді. Басқаша айтқанда, осы аймақта екі фаза - сұйық және газ - бірдей тіршілік етеді.
Өз сұйығымен динамикалық тепе-теңдікте болатын бу қаныққан бу д. а.
Қаныққан бу қысымы көлемге тәуелсіз. Қаныққан бу қысымының температураға тәуелділігі төмендегі суретте көрсетілген

Ауадағы су буының мөлшері ауаның ылғалдылығы д. а.
Ауаның абсолют ылғалдылығы дегеніміз ауа құрамындағы су буының парциал қысымы.
Берілген температурада ауа құрамындағы су буының  парциал қысымының, сол температурадағы қаныққан будың
парциал қысымының, сол температурадағы қаныққан будың 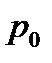 қысымына, пайызбен өрнектеліп алынған қатынасы, ауаның салыстырмалы ылғалдылығы деп аталады:
қысымына, пайызбен өрнектеліп алынған қатынасы, ауаның салыстырмалы ылғалдылығы деп аталады:
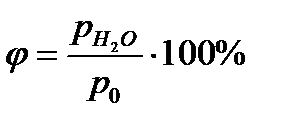
Билет.
Молекулалық физиканың мәселесі. Статистикалық және термодинамикалық әдістер. Материялық денелердің молекула-кинетикалық үлгісі. Атомдар мен молекулалардың массасы.
Молекулалық физика – физиканың әр түрлі агрегаттық күйдегі заттардың физикалық қасиеттерін олардың молекулалық құрылысы негізінде зерттейтін саласы. Молекулалық физиканың ең алғаш қалыптасқан бөлімі – газдардың молекулалық-кинетикалық теориясы. Бұл теория 1858 – 60 жылдары Дж.Максвеллдің, 1868 жылы Л.Больцман және 1871 – 1902 жылдары Дж.Гиббс еңбектерінің нәтижесінде классикалық - статистикалық физика болып қалыптасты. Молекулалардың өзара әсері (молекулалық күштер) жөніндегі сандық мәліметтер капиллярлық құбылыстар теориясында: 1743 жылы А. Клероның, 1805 жылы Т.Юнгтың, 1806 жылы П.Лапластың, С.Пуассонның, т.б-дың классикалық еңбектерінде дамытылып, беттік құбылыстар теориясының жасалуына негіз болды. Голланд физигі Я.Ван-дер-Ваальс нақты газдар мен сұйықтықтардың физ. қасиеттерін түсіндіру үшін молекула аралық өзара әсер ұғымын (1873) пайдаланып нақты газдардың күй теңдеуін (Ван-дер-Ваальс теңдеуі) қорытып шығарды. 1906 жылы француз физигі Ж.Перрен мен швед ғалымы Т.Сведбергтің, 1904 – 06 жылы поляк физигі М.Смолуховский мен А.Эйнштейннің микробөлшектердің броундық қозғалысына және заттардың молекулалық құрылысына арналған зерттеу жұмыстары кез келген заттың молекулалардан тұратындығының айғағы болды. Кванттық механикада молекула аралық өзара әсер туралы ілім 1927 жылы Ф.Лондонның, 1927 жылы В.Гейтлердің, 1930 жылы П. Дебайдың, 1937 – 39 жылы М.Борнның еңбектерінде дамытылды. 19 ғасырда Я.Ван-дер-Ваальс пен У.Томсон (Кельвин) байқаған және Дж.Гиббс пен 1937 жылы Л.Ландаудың еңбектерінде дамытылған бір агрегаттық күйден екінші агрегаттық күйге ауысу теориясы фаза түзілудің қазіргі теориясына айналды; сөйтіп ол молекулалық физиканың маңызды жеке тарауы болып қалыптасты. Я.И. Френкельдің, Дж.Берналдың, т.б. еңбектерінде статистик. әдістің заттардың құрылымы жөніндегі көзқараспен біріктірілуі сұйықтықтар мен қатты денелердің молекулалық физикасының дамуына үлкен әсер етті. Мұнда газдардың, сұйықтықтардың және қатты денелердің құрылысы, олардың сыртқы әсерлердің (қысым, темп-ра, электр және магнит өрістері) нәтижесінде өзгеруі, тасымалдау құбылысы (диффузия, жылуөткізгіштік, ішкі үйкеліс), фазалық тепе-теңдік және ауысу процестері (кристалдану және балқу, булану және конденсация, т.б.) заттардың кризистік күйі, әр түрлі фазалардың бөліну шекараларындағы беттік құбылыстар қарастырылады. 20 ғасырда молекулалық физиканың жедел қарқынмен дамуы нәтижесінде одан статистикалық физика, физ. кинетика, қатты денелер физикасы, физ. химия тәрізді ірі, өз алдына дербес салалар бөлініп шықты.Заттардың және олардың зерттеу әдістерінің әр түрлі болуына қарамастан молекулалық физика заттар құрылысының микроскопиялық (молекулалық) сипатына негізделе отырып, олардың макроскопиялық қасиеттерін зерттейді
Жуйенің күйін термодинамикалық және статистикалық амалдарды қолданып зерттейді. Термодинамикалық амалдар жүйенің ішкі құрылымын ескермей қарастырады. Осы кезде түсініктер мен шамалар тұтас жүйеге қатысты қолданылады. Статистикалық амал орасан көп бөлшектерден тұратын жүйелі динамикалық жолмен сипаттау мүмкін емес. Макрожүйелерді зерттегенде жеке бөлшектерге емес, көптеген бөлшектер жиынтығына қатысты түсініктер мен шамаларды қолданатын статистикалық әдістер пайдаланылады. Процесс деп бір тепетең күйден басқасына көшуді айтады. Релаксация жүйенің тепетең күйіне қайтып оралуы.
Молекула – заттың қасиетін сақтайтын, ең кіші бөлшек. Атом – хим.элементтің хим.қасиеттеріне ие болатын ең кіші бөлшек. Әртүрлi денелер молекуласының масса бiрлiгi ретiнде 12С көмiртегi изотобы атомының moc массасының 1/12 бөлiгi алынады. Ол атомдық масса бiрлiгi (а.м.б. ) д.а және мынаған тең:
1 а.м.б. =1,66·10-27 кг. (1.1)
Заттың салыстырмалы молекулалық массасы МR деп заттың бiр молекула m0 массасының көмiртегi атомы moc массасының 1/12 бөлiгiне қатынасын айтады:
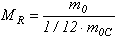 (1.2)
(1.2)
Зат мөлшерi деп берiлген жүйенiң бөлшектерiнiң, құрылымдық элементерiнiң, санына пропорционал ν шаманы айтады. Оны моль арқылы жазу қабылданған. Массасы 0,012 кг 12С көмiртегiнде қанша атом болса, сонша молекуладан (атомнан) тұратын зат мөлшерi бiр моль деп аталады. Бұл сан Авогадро тұрақтысы деп аталады және NA арқылы белгiленедi:
NA ≈ 6·1023 моль-1. (1.3)
Сәйкесiнше, кез келген заттың 1 молiнде атомдар саны мен молекулалар саны бiрдей болады. Егер денедегi зат мөлшерi ν мольден тұрса, онда денедегi молекулалар N саны мынаған тең:
N = ν · NA. (1.4)
Заттың молярлық массасы М деп бiр моль мөлшерiнде алынған зат массасын айтады. Ол бiр молекула массасының m0 Авогадро санына NA көбейтiндiсiне тең:
М = m0· NA кг/моль. (1.5)
Молярлық және молекулалық массалар арасында мынадай қарапайым байланыс бар:
М = 10-3 ·Мr кг/моль. (1.6)
Кез келген зат мөлшерiнiң m массасы бiр молекуланың массасын денедегi молекулалар санына көбейткенге тең:
m = m0· N кг. (1.7)
(1.5) және (1.7) формулаларын пайдаланып (1.4) өрнегiнен мынаны алу қиын емес:
ν = m / М және N = ν·NA = NAA ·m / M. (1.8)
Бөлшектердiң массасымен өлшемдерiн қосымша тәжiрибелiк деректердi пайдалана отырып есептеуге болады. Жеке жағдайда, молекулалардың сызықты өлшемдерiн бағалауға болады.
Молекуланың өлшемiн былайша анықтауға болады. Бiр молекуланың алатын V0 көлемi зат V көлемiнiң, ондағы молекулалар N санына қатынасына тең: 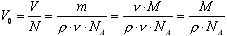 , мұнда ρ=m/V – заттың тығыздығы. Молекуланың формасы радиусы r шар тәрiздес болсын. Сондықтан
, мұнда ρ=m/V – заттың тығыздығы. Молекуланың формасы радиусы r шар тәрiздес болсын. Сондықтан 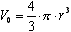 . Осыдан:
. Осыдан:
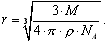 (1.9)
(1.9)
Мысалы, су молекуласының радиусы мына шамаға тең:
 .
.
Билет.
Қатты денелер. Заттың кристалдық және аморфтық күйі. Кристалдарды жіктеу. Қатты денелердің жылусыйымдылығы. Жылусыйымдылықтың классикалық теориясы. Дюлонг және Пти заңы.
Қатты денелер.
Біз қатты дене жершарының бетінде, қатты денелерден салынған құрылыстарда-үйлерде өмір сүріп жатырмыз. Біздін денемізде шамамен 65% су болғанын өзіде (майда 80%) ол катты денеге жатады. Қатты денелердің қасиеттерін білу тіршілік үшін қажет.Қатты денелер сұйықтар сияқты өзінің көлемін ғана сақтап қоймады, сонымен бірге пішінін де сақтай алады. Бірақ олар өздеріне түсірілген күштердің әсерінен пішіндерін өзгертеді, яғни деформацияланады.Дене пішінін немесе көлемінің өзгеруі деформация д.а(Резеңке бау).Сыртқы күштер әсері тоқталғанан кейін толық жойылатын деформациялар серпінді деформациялар д.а.Пластикалық су балшықта пластилинде немесе қорғасында серпінді деформациялар аймағы аз шағын жүктің өзі пластикалық деформациялар тудыратын материялдарды пластикалық материялдар деп атайды.Егер материал болмашы деформацияларда қирап бөлінетін болса ол материал морт д.а(шыны,фарфордан жасалғын бұйымдар). Олар негізінен кристал күйде болады екен.
Кристалдар -атомдары немесе молекулалары кеністікте белгілі орындалып, реттеліп орналасқан қатты денелер. Кристалдың сыртқы пішіні дұрыс яғни бірқалыпты болуында(кәдімгі ас тұзы түйіршігі).
Кристалдық күйлердің айрықша белгілері.
Табиғаттағы денелердің көпшілігінің құрлымы кристалдық болып саналады(барлық минералдар н/е барлық талдар қатты күйінде кристалл болып табылады).Бірақ сыртқы пішіні дұрыс болып келуі кристалдық реттелген құрылысының жалғыз ғана ең басты салалары бола алмайды. Бастысы-физикалық қасиеттердің кристалды таңдалып алынған бағытқа тәуелділігі. Ең алдымен, кристалдық механикалық біріктірігінің әртүрлі бағытта түрліше болатыны көзге түседі.Барлық бағыттар бойынша қасиеттері бірдей болатын денелерді изотопты д.а. Кейбір газдар мен сұйықтардаң басқа барлық сұйықтар н/е оларды қатты денелер изотопты болып саналады. Кристалдың анизатроптылығын оны құрайтын бөлшектердің белгілі тәртіпен орналасуымен түсіндіруге болады. Кристалдың сыртқа беделдерінің дұрыс болуының бөлшектерінің тәртіппен орналасуымен түсіндіріледі.Физикалық қасиеттердің кристал ішіндегі бағыттарға тәуелділігі анизатропия д.а. Кристал денелер монокристалдар және поликристалдар болып бөлінеді.
Не нашли, что искали? Воспользуйтесь поиском: