
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Жылу двигателi. Карно циклi 4 страница
Идеал газдың изобаралық және изохоралық процестері кезіндегі мольдік жылу сыйымдылықтары арасындағы байланысты тұңғыш рет Р.Майер тағайындады, ол  . Бұл формула Майер формуласы деп аталады. Қоршаған ортамен жылу алмасуынсыз өтетін процестерді адиабаталық процесс деп атайды. Адиабаталық процесс кезінде Q=0 және термодинамиканың І заңы бойынша A=DU. Адиабаталық процесс Пуассон теңдеуімен сипатталады:
. Бұл формула Майер формуласы деп аталады. Қоршаған ортамен жылу алмасуынсыз өтетін процестерді адиабаталық процесс деп атайды. Адиабаталық процесс кезінде Q=0 және термодинамиканың І заңы бойынша A=DU. Адиабаталық процесс Пуассон теңдеуімен сипатталады:  . Мұндағы
. Мұндағы 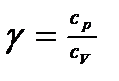 Адиабаталық процесс кезiнде жылу алмасу болмайды. Сонда жүйенiң iшкi энергиясы тек қана онымен жасалған жұмыстың есебiнен өзгередi. Адиабаталық процесс жүретiндей етiп, белгiлi бiр тұрақты температураны алыңыздар да, жұмыс жасалуына қарай газдың iшкi энергиясының қалай өзгеретiндiгiн бақылаңыздар. Адиабаталық процесс кезiнде Q = 0 және жүйенiң iшкi энергиясының өзгеруi жұмыс атқару арқылы ғана жүредi: ΔU = А. ΔU = А теңдiгi белгiлi қорытынды жасауға мүмкiндiк бередi. Егер жүйеде оң жұмыс жасалса, мысалы газ сығылатын болса, онда оның iшкi энергиясы ұлғаяды және температурасы өседi. Керiсiнше, газ ұлғайған кезде, ол өзi оң жұмыс атқарады (Аұ > 0). Оның iшкi энергиясы азаяды да, газ суиды.
Адиабаталық процесс кезiнде жылу алмасу болмайды. Сонда жүйенiң iшкi энергиясы тек қана онымен жасалған жұмыстың есебiнен өзгередi. Адиабаталық процесс жүретiндей етiп, белгiлi бiр тұрақты температураны алыңыздар да, жұмыс жасалуына қарай газдың iшкi энергиясының қалай өзгеретiндiгiн бақылаңыздар. Адиабаталық процесс кезiнде Q = 0 және жүйенiң iшкi энергиясының өзгеруi жұмыс атқару арқылы ғана жүредi: ΔU = А. ΔU = А теңдiгi белгiлi қорытынды жасауға мүмкiндiк бередi. Егер жүйеде оң жұмыс жасалса, мысалы газ сығылатын болса, онда оның iшкi энергиясы ұлғаяды және температурасы өседi. Керiсiнше, газ ұлғайған кезде, ол өзi оң жұмыс атқарады (Аұ > 0). Оның iшкi энергиясы азаяды да, газ суиды.
Политроптық процестер. Осыған дейін қарастырылған изобаралық, изохоралық және адиабаталық процестерге тән ортақ қасиет бар. Ол - процестер барысында дененін, жылусыйымдылығының өзгермей,тұрақты болып қалатындығы.Мұндай, дененің жылусыйымдылығы тұрақты болып қалатын процесс политроптық д.а. Енді осы процестерді сипаттайтын ортақ тендеуді анықтайық.Аныктама б/ша, кезкелген политроптық процесс үшін дененің жылусыйымдылығы тұрақты болады. Олай болса, мұндай процесс үшін термодинамиканың бірінші бастамасы


болып жазылады. Бұл теңдеудегі газдың күйін анықтайтын үш шама да (р, V, Т) айнымалы. Клапейрон-Менделеев тендеуін пайдаланып,
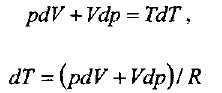
деп табамыз (газдың бір молі үшін). Мұны апарып, политропа үшін жазылған термодинамиканың бірінші бастамасының тендеуіне қойып, интегралдап, политропа теңдеуін аламыз:
 Бұл жерде біз
Бұл жерде біз 
15 билет.
Адиабаталық процесс. Пуассон теңдеуі. Политропты процесс.
Адиабаталық процесс қоршаған ортамен жылу алмаспайтын физикалық жүйеде өтетін термодинамикалық процесс.Адиабаталық процесс жылу өткізбейтін (адиабаталық) қабықшалармен қоршалған жүйелерде өтеді деп есептелінеді.Сыртқы орта мен жүйе арасында жылу алмасып үлгере алмайтындай уақытта тез өтетін процестер (жылу оқшаулағыш қабықшалары болмайтын) адиабаталық процесс ретінде қарастырылады. Оған мысалы, дыбыстың ауада таралуы, жылу қозғалтқыштарының цилиндрі ішіндегі газдың сығылуы (немесе ұлғаюы) т.б. жатады. Газ сығылғанда температура көтеріледі, ұлғайғанда — төмендейді. Адиабаталық процесс қайтымды және қайтымсыз процесс түрінде өтуі мүмкін. Адиабаталық процесс - атмосферада адиабаталық процесс — қоршаған ортамен жылу алмасуынсыз болып тұратын (жер бетімен, ғарышпен, жанасатын ауа массасымен) ауаның термосерпіндік өзгерісі
Адиабаталық процесс кезiнде Q = 0 және жүйенiң iшкi энергиясының өзгеруi жұмыс атқару арқылы ғана жүредi: ΔU = А. ΔU = А теңдiгi белгiлi қорытынды жасауға мүмкiндiк бередi. Егер жүйеде оң жұмыс жасалса, мысалы газ сығылатын болса, онда оның iшкi энергиясы ұлғаяды және температурасы өседi. Керiсiнше, газ ұлғайған кезде, ол өзi оң жұмыс атқарады (Аұ > 0). Оның iшкi энергиясы азаяды да, газ суиды.
Адиабаталық процесс үшін d’Q=0, онда ТД-1з жазылуы d’A= -dU(1), яғни ад.процесс кезіндегі жуйенің жұмысы ∆U арқ жүреді. d’A=PdV және dU=CvdT өрнектерін ескеріп 1-ны былай жазамыз. PdV=-CvdT.
Адиабаталық процесс кезінде газдың қысымы мен оның көлемі арасындагы байланыс Пуассон теңдеуі арқылы көрсетіледі р  = const,
= const,
яғни  , мұндағы
, мұндағы  .
.
Пуассонның теңдеуін мынандай түрде де жазуға бо лады:  ,
,
яғни 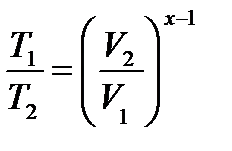 , немесе
, немесе  , яғни
, яғни  .
.
Газдың көлемі адиабаталы өзгергенде істелетін жұмысты төмендегі формуламен табуға болады:
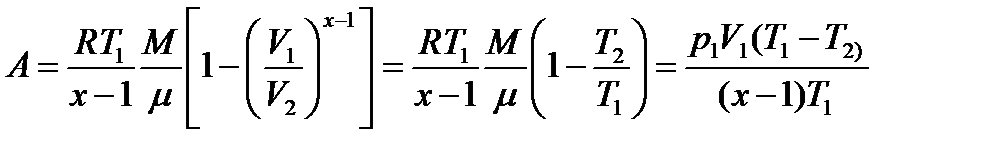
Политропиялық процесс теңдеуінің түрі төмендегідей болады:  ,
,
немесе  мұндағы п — политропа көрссткіші (1<
мұндағы п — политропа көрссткіші (1<  < х).Жылу машинасыпың пайдалы әсер коэффициенті
< х).Жылу машинасыпың пайдалы әсер коэффициенті  ,
,
мұндағы Q1 — жұмысшы денеге берілген жылу, ал Q2 —'суытқышқа берілген жылу. Карноның идеал циклі үшін 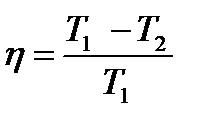
мұндағы,Т1— қыздырғыштың температурасы, Т2 — суытқыштың температурасы.
В мен А екі күйдің энтропияларының айырымы sв — sа төмендегі формуламен анықталады:  .
.
Изотермиялық және адиабаталық процестер деп – идеал пр-тер, оларды практикада жүзеге асыру мүмкін емес, оларға тек жақындауға ғана болады. Изот.процесс ∞ баяу жүру керек, ал адиаб.процесс шекті жылдамдықпен жүргенімен, адиабаталық қабықшада жүру керек және ең бастысы оның жылу өтімділігі ≈0 болу керек. Бұлай болу мүмкін емес. Табиғатта ад-лық және изот. пр-дің аралығында өтетін нақты пр-тер жүреді. Мұндай пр-тер политропты процестер деп аталады.Бұл процессте дененің Т↑ денеге берілген d’Q-ке пропорционал, яғни политропты процесс ушін C=const, сонымен политропты процесс деп газдың жылусыйымдылығы тұрақты болатын процессті айтады. Бұрын қарастырған барлық процесстер политропты процесстің дербес жағдайлары деп есептеуге болады. Пуассон теңдеуі сәйкес үш теңдеудің политропты процесс үшін жазылуы:
PVn=const
TVn-1=const
TnP1-n=const
n- пол.корсеткіші
n=0 изоб.процесс
n=1 изот.процесс
n=ᵧ адиаб.процесс
n=±∞ изох.процесс орындалады.
Политропты процесс дегеніміз, жылуды қалай болса солай жеткізу немесе алып кету (dqа≠0) процессін айтады, ол үшін көрсеткіштерінің өзара байланыстылығының теңдеу түрі:
· Pνn" = const,
мұндағы n - политроптың көрсеткіші. Дәл осы, қайтымды политропты өзгерту күйінің көрсеткіші n, процесстің барлық нүктелері үшін белгілі, тұрақты шамада болады.
n= 1 pν = const кезінде, яғни изотермиялық процесстің теңдеуі болады, n = k, Pνk = const - адиабатты (изоэнтропиялық) процесс кезінде болуы. Әр түрлі политропты көрсеткіштер үшін, политроп жағдайы суретте көрсетілген.
Политроптар үшін, жұмысқа арналған формулалар мен көрсеткіштер, аралық байланысы қалтқысыз болуы да, изоэнтропиялық процесспен ұқсас. Тек қана, изоэнтропты көрсеткішті k, политропты көрсеткішпен n алмастыру ғана қалды. Сонымен, жұмыстың көлемнен өзгеруі, мынаны құрайды:

және 
Изохорлы және изобарлы процесстерді, жеке күй ретінде қарастырылуы мүмкін:
· изохорлы процесс үшін n = ∞ және p1/∞ν = ν = const,
· изобарлы процесс үшін pν°=р = const.
Политропты процесстегі, газдың меншікті санды жылулығы, мына жолмен алынуы мүмкін:
· 
Жоғарыдағы теңдеулерді есепке алғандағысы:
· 
немесе Cp - Cν = R кезінде
· 
Бұдан, идеалды газға арналған, қайтымды политропты процесстің меншікті жылу сыйымдылығын табамыз:
· 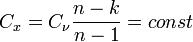
Себебі, Cν= const, const және n = const. Сонымен, қайтымды политропты процесс, тұрақты меншікті жылу сыйымдылығының процессі.
Билет.
Газдардағы тасымалдау құбылыстары:диффузия,тұтқырлық(ішкі үйкеліс), жылуөткізгіштік. Молекулалардың еркін жолының орташа ұзындығы
Тасымалдау Құбылыстары – физикалық жүйеде электр заряды, масса, импульс, энергия, энтропияның, т.б. физикалық шамалардың кеңістікте тасымалдануы (бөлінуі) арқылы өтетін кинетикалық процестер. Тасымалдау құбылыстарына жылу өткізгіштік, диффузия, ішкі үйкеліс жатады. Газ ағыны ХY жазықтығына параллель оң бағытта қозғалсын. Ламинарлық қозғалыста оның u жылдамдығы Z осі бойынша өзгеріп отырады және соның себебінен,газдың көршілес қабаттарының арасында әсерлесу күштері пайда болады.Осы күштер ішкі үйкеліс күштері д.а.ж/е олар қабаттар жанасатын ауданға,газ ағынының жылдамдық градиентіне du/dz тура пропорционал:
Пропорционалдық коэффициент η - ішкі үйкеліс коэффициенті д.а. ж/е оның өлшем бірлігі пуазель(Пуаз),1Пуаз=0,1Па*с. Жылдамдық градиенті,оның Z осі б/ша өзгеру тездігін сипаттайды.
Жылу өткізгіштік

 Егер газ қабаттарының температурасы әртүрлі болса, онда температурасы жоғары қабаттан төмен қабатқа жылу ауысады.Бұл процесс жылу өткізгіштік д.а. Газдан бөлінген көлемдегі температура Z осімен өзгереді деп саналсын.Екі газ қабатын бөлетін dS ауданның үстінің температурасы жоғары, астының температурасы төмен болсын. Сонда жоғарғы қабаттан төменгісіне ауысатын жылу мөлшері dS ауданға, dt уақытқа және - жылдамдық градиентіне тура пропорционал,
Егер газ қабаттарының температурасы әртүрлі болса, онда температурасы жоғары қабаттан төмен қабатқа жылу ауысады.Бұл процесс жылу өткізгіштік д.а. Газдан бөлінген көлемдегі температура Z осімен өзгереді деп саналсын.Екі газ қабатын бөлетін dS ауданның үстінің температурасы жоғары, астының температурасы төмен болсын. Сонда жоғарғы қабаттан төменгісіне ауысатын жылу мөлшері dS ауданға, dt уақытқа және - жылдамдық градиентіне тура пропорционал,
яғни,
(1.1)
Пропорционалдық коэф. х – жылу өткізгіштік коэф д.а және оның өлшем бірлігі Вт/м*К.
Жылу өткізгіштік коэф-ң сан мәні газдың тегіне және күйіне тығыз байланысты.
Диффузия
 Диффузия(лат. таралу, жайылу) – нақтылы дене бөлшектерінің жылулық қозғалыстарға ұшырай отырып,сол дене концентрациясының селдір аудандарына қарай
Диффузия(лат. таралу, жайылу) – нақтылы дене бөлшектерінің жылулық қозғалыстарға ұшырай отырып,сол дене концентрациясының селдір аудандарына қарай
жылжуы;молекулалардың жылулық қозғалысы салдарынан шекаралас орналасқан әр түрлі заттардың бір-біріне өту құбылысы. Диффузия дененің бүкіл көлеміндегі концентрация мөлшерінің бірте-бірте теңелуін, сөйтіп оның бірқалыпты сипат алуын қамтамасыз етеді. Кейбір денелердің өте шағын бөлшектері ғана емес (атомдар,молекулалар, иондар), біршама ірі түйіршіктеріде диффузиялық қасиетті иемденуі мүмкін. Диффузия жылдамдығы температураға тікелей байланысты, алайда бұл процесс газдарда өте тез, сүйықтарда одан гөрі баяу, ал қатты заттарда өте баяу өтеді.
Диффузия қоспалы газдарда ғана емес, егер газдың берілген көлемдегі концентрациясы біркелкі болмаса, біртекті газдардада жүреді.
 мұнда
мұнда  себебі
себебі  = p0 тығыздықты береді.Осыдан диффузия салдарынан ауысатын газ массасы мынаған тең:
= p0 тығыздықты береді.Осыдан диффузия салдарынан ауысатын газ массасы мынаған тең:  , масса теңдеулерін салыстыру арқылы диффузия коэфиценті анықталады:
, масса теңдеулерін салыстыру арқылы диффузия коэфиценті анықталады: 

Пропорционалдық коэфициент D- диффузия коэфициенті деп аталады және ол газдың қасиеттеріне ғана емес, сонымен қатар, ортаның да күйіне,табиғатына,тығыздығына көп тәуелді. Диффузия коэффициентінің өлшем бірлігі м2/с. Еркін жол ұзындыгы, орташа еркін жол ұзындығы()—бөлшектердің өзі тәрізді басқа бөлшектермен тетелес екі соқтығысуы арасында жүріп өткен жолы. Соқтығысу түріне (серпімді, серпімсіз, т.б.) байланысты Е. ж. ұ. түрліше болып келеді. “Е. ж. ұ. ” ұғымы алғаш рет газдың кинетикалық теориясында қолданылды. Егер бірқалыпты және түзусызықты қозғалған газ молекуласы 1с ішінде өзінің жылдамдығына (u) тең жол жүре отырып, n рет серпімді соқтығысса, онда орташа Е. ж. ұ. былай анықталады: u/n=1/(ns), мұндағы n — бірлік көлемдегі молекула саны (газ тығыздығы), s — молекулалардың эффективтік қимасы. Қалыпты жағдайда газ молекулаларының Е. ж. ұ. () шамамен 10–5 см болады. Е. ж. ұ. тұтқырлық, жылу өткізгіштік, диффузия, электр өткізгіштік тәрізді тасымалдау процестеріне байланысты есептерді шешкенде кеңінен қолданылады.Зарядталған бөлшектердің (электрондар мен иондардың) Е. ж. ұ-н қарастырғанда тиімді қима ұғымының мәні болмайды.Өйткені иондар (электрондар) атомдармен (молекулалармен) қашықтан да әсерлесе береді.
Билет.
Молекулалар жылдамдықтарының Максвелл бойынша таралуы. Орташа квадрат, орташа арифметикалық және ықтимал жылдамдықтар.
Молекулалардың жылдамдықтары еш уақытта да бірдей бола алмайды, тәжІрибелер де осыны дәлелдейді. Молекулалардың ретсіз қозғалыстарының және олардың бір-бірлерімен соқтығысуларының арқасында газ молекулалары қандай да болмасын бір жолмен жылдамдықтар бойынша таралады, демек олардың ішінде оте жеделдері де, өте баяулары да болады. Молекулалардың қозғалыстарының толық хаостығына, олардың соқтығысуларын және осыдан пайда болатын молекулалар жылдамдықтарының өзгерістерінің кездейсоқтығына қарамай, молеулалардық жылдамдықтар бойынша таралуы кездейсоқ түрде емес, белгілі заңға бағынады. Оның сипатына молекулалар арасында болатын соқтығысулар да, сыртқы күш орістері де әсер етпейді, ол әркашан бір мәнді жөне бір-ақ түрде болады екен. Тәжірибе де осылай дейді.
Сонымен молекулалардың жылдамдықтар бойынша таралуы деп нені түсінеміз? Берілген жылдамдықтын маңындағы қайсы-бір интервалдағыдай жылдамдықтарға ие болатын молекулалардың саны (немесе салыстырмалы үлесі) қандай болады? Статистикалык мәселелер міне осылай қойылады.
1. Статистикалық тепе-теңдік күйі кезінде газ молекулаларының жылдамдықтарының барлық бағыттары бірдей ықтималдыкта болады. Егер олай бол-маған жағдайда газдың жылулық қозғалысы толық бей-берекет болмаған бо-лар еді. Осы күйдегі молекулалардың барлық жылдамдықтарының абсолют шамалары да бірдей бола алмайды. Кездейсоқ қайсы-бір мезетте олар бірдей болып
шыққан жағдайда да, келесі мезетте бүл күй молекулалардың өзара соқтығысуы әсерінен бүзылған болар еді.
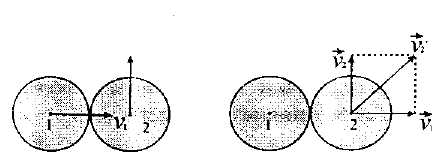
| Көрнекірек болу үшін тек бір-бірімен соқты-ғысьш қалған кезде ғана өзара әрекеттесетін идеал серпімді және тегіс шариктерден гүратын қарапайым газ моделін қарастырайык. Соқтығысуға дейінгі V1 және V2 жылдамдықтары өзара перпендикуляр болатын 1 және 2 молекулалар озара соктығысты делік Бірінші молекула 12 центрлер сызығы бойымен, ал екіншісі оған перпендикуляр қозғалсын делІк. Шариктер абсолют жылтыр болатындықтан, соқтығысу кезінде олардың жылдамдықтарының жанама қүраушысы өзгеріссіз қалады. Бірақ шариктер абсолют серпімді соқтығысу заң-дылықтарына сай, нормал жылдамдыктарымен ал-масуы тиіс. Соқтығысудан кейін бірінші шарик тоқтайды, екінші шариктің жылдамдығы ΔV2 =V1 |
 Молекулалардың озара өрекеттесулерінен олардың жылдамдықтары өзгеріп отырады. Бірақ қаншалықты кішкентай көлем элементін алғанымыз-бен, ондағы молекулалар саны өрқашанда орасаң зор болады да, оның кез-келген уақыт мезетіндегі өзгерістерін ескерімсіз аз деп санауға болады. Бұл тоқтам газ молекулаларының санының орасан зор болатындығының арқа-сында өрқашанда орындалады.
Молекулалардың озара өрекеттесулерінен олардың жылдамдықтары өзгеріп отырады. Бірақ қаншалықты кішкентай көлем элементін алғанымыз-бен, ондағы молекулалар саны өрқашанда орасаң зор болады да, оның кез-келген уақыт мезетіндегі өзгерістерін ескерімсіз аз деп санауға болады. Бұл тоқтам газ молекулаларының санының орасан зор болатындығының арқа-сында өрқашанда орындалады.
жыдамдық нүктелердің орташа концентрациясын білдіреді жөне ол байырғы (координаттық) кеңістіктегі бөлшектердің концентрациясына үқсас деуге болады. і"(у) шамасы молекулалардың жылдамдықтар бойынша таралу фуикциясы деп аталады. Оны молекулалардың жылдамдықтар нүктелерінің жылдамдықтар кеңістІгінде таралу ықтималдығының тығыздьіғы деп түсінуге болады. Молекулалардың жылдамдықтар бойынша таралуы статистикалық

мәселесі міне осы і*(у) функцияны анықтауға әкеледі.
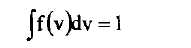
|
Ықшамдық үшін молекуланың

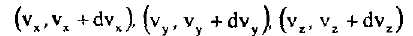
|
 жылдамдық интервалдарына түсуін сөйкес түрде А,В,Соқиғалар деп атаймыз. Мүндай түсу күрделі оқиға, ол А,В,С оқиғалардың көбейтіндісі болып табылады. Оның ықтималдыгын ықтималдықтарды көбейту теоремасы бойынша анықтауға болады. Бүл үшін А оқиғаның ықтималдығын А оқиға болып отгі деп есептеп, В оқиғаның шартты ықтималдығына көбейгу керекте, содан кейін нәтижесін, А жоне В оқиғалар болып отті деп есептеп, С оқиғаныңшартты ықтималдығынакобейту керек.Максвелл А,В,С оқиғалар-ды твуелсіз деген болжам жасады. Бүл жағдайда ықтималдықтарды көбейіу теоремасын тәуелсіз оқиғалар үшін деп, оның қарапайым түрінде жүргізуге болады.
жылдамдық интервалдарына түсуін сөйкес түрде А,В,Соқиғалар деп атаймыз. Мүндай түсу күрделі оқиға, ол А,В,С оқиғалардың көбейтіндісі болып табылады. Оның ықтималдыгын ықтималдықтарды көбейту теоремасы бойынша анықтауға болады. Бүл үшін А оқиғаның ықтималдығын А оқиға болып отгі деп есептеп, В оқиғаның шартты ықтималдығына көбейгу керекте, содан кейін нәтижесін, А жоне В оқиғалар болып отті деп есептеп, С оқиғаныңшартты ықтималдығынакобейту керек.Максвелл А,В,С оқиғалар-ды твуелсіз деген болжам жасады. Бүл жағдайда ықтималдықтарды көбейіу теоремасын тәуелсіз оқиғалар үшін деп, оның қарапайым түрінде жүргізуге болады.
Сонымен, молекуланың жылдамдыктык нүктесінің бір мезгілде үш интервалдарда болуы ықтималдығы
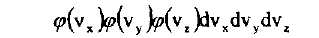
Кобейтіндісімен берілуі тиіс және таралу функциясының түрінің

| Ғ(у) функция міне осы шартты канағаттандыруы тиіс. |
болатындығына келеміз. Газда координат өстерінің оң және теріс бағыттарында еш айырмашылық жоқ. жылдамдықтың тек модуліне ғана басқаша айтсақ, квадратына ғана төуелді бола алады. Дәл осылай, газдың изотропиясының арқсында Г функция да тек V толық жылдамдықтың квадратына ғана төуелді бола алады, бірақ оның бағытына тәуелсіз болады. Жылдамдықтардың квадраттарының орнына аргумент ретінде сәйкесинетикалық энергияларды алган ыңғайлырақ болады:

Жаңа аргументтерге көшкен кезде функциялардың өздерін бүрынғыша белгілей береміз, бірақ, шын мәнісінде, аналитикалық түрғыдан бүлар басқа функциялар. Сонда тендеу мына түрде жазылады:
 Осыдан
Осыдан
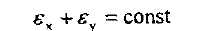 шарты кезінде
шарты кезінде
 болатындығы шығады. Екінші қатынасты әуелі дифференциалдап, сосын погарифмде
болатындығы шығады. Екінші қатынасты әуелі дифференциалдап, сосын погарифмде
 шарты орындалатын кезде
шарты орындалатын кезде
деп аламыз. Осыдан:
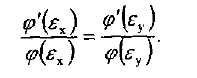 функциясы
функциясы
Олардың арасындағы тендік тек 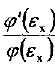 және
және  қатынастары бір ғана түрақтыға тең болатын кезде ғана орындалады. Осы түрақтыны - а деп белгілеп,
қатынастары бір ғана түрақтыға тең болатын кезде ғана орындалады. Осы түрақтыны - а деп белгілеп,

деп, немесе осІмше алады. Бүл мысал соқтығысу кезінде молекулалардың қозғалыс бағыттары ғана емес, сонымен қатар олардың жылдамдықтарының абсолют мөндері де өзгереді дегенді көрсетеді. Қарастырылған соқтығысу мүмкіндіктердің біреуі ғана. Шындығына келсек, соқтығысулар түрлері сан-алуан. Олар жыл-дамдықтардың өзгерістерінің сан-алуан мүмкіндіктерін тудырады да, ақыры молекулалардың жылдамдықтар бойынша белгілі түрдегі статистикалық таралуына алып келедІ.
Газ молекулаларының жылдам-дықтар бойынша таралуы мөселесін Максвелл қойып, ол оны 1859 жылы шешті.. Молекулалардың жылдамдықтар бойынша таралуын статис-тикалық мәселе деп қарастыру керек. Оны былай түжырымдауға болады.Жылдамдықтар кеңістігінде физикалық түрғыдан шексіз аз көлем элементін,
мысалға,

|

| деп аламыз. Интегралдағаннан кейін: |
рвалда бола-тын молекулалардың ықтимал
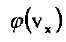
|
мүндағы А, - жаңа түракты, оның мөнін томенде анықтаймыз. а тұрақты
Не нашли, что искали? Воспользуйтесь поиском: