
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Жылу двигателi. Карно циклi 2 страница
Егер дене бір кристалдан тұрса,оны монокристал д.а. Кейбір менералдардың монокристалдары табиғатта табиғи күйінде кездеседі.
Ұсақ кристалдарды бір-біріне жабысып орналасуын поликристал д.а.Поликристалл денелердің түзілу себебі – көптеген кристалдардың өсуі. Олар бір-біріне жақындап, тиіскен кезіне дейін жалғаса береді де, осының нәтижесінде біртұтас дене түзіледі (кесек қантның құрылымы)
Кристалдың өзі құрылымдық элементтің үш әр түрлі бағыт бойынша, көп ретті қайталануынан алынады. Ол құрылымдық элементті элементтар кристалдық ұя деп атайды.
Аморф денелер.
Аморф денелер – кристалл қатты денелер мен сұйықтардың арасында аралық орын алады. Олардың атомдары мен молекулалары салыстырмалы ретте орналасқан.Қатты денелердің барлығын кристалл денелерге жатқызуға болмайды.Аморф денелерде атомдардың дәлме-дәл ретті орналасуы жоқ. Тек жақын көрші атомдар реті белгілі бір ретпен орналасады.Бірақ кристалдарға тән құрылымның қандай да бір элементінің барлық бағытта дәлме-дәл қайталануы аморф денелерде болмайды.Көпшілік жағдайда бір заттың өзі кристалдық күйде де, аморф күйде де бола алады. Мысалы, кварц Si O2 кристалды түрде және аморфты түрде бола алады. Кварцтың кристалдық түрін бұрыс алты бұрыштан тұратын тор деп қарастыруға болады. Кварцтың аморфты құрамы да тор тәрізді, бірақ дұрыс пішінде емес. Онда алтыбұрыштармен қатар, бесбұрыштар және жетібұрыштар кездеседі.
Аморф денелердің қасиеті.
Барлық аморф денелер изотропты, олардың физикалық қасиеттері барлық бағыты бірдей. Аморф денелерге шыны, көптеген пластмассалар, смола, қант мұздығы (мөлдір кәмпит) т.б жатады. Сырттан әсер еткенде аморф денелерде қатты денелердегі сияқты серпінділік қасиеті және сұйықтағы сияқты аққыштық қасиеті де бір мезгілде байқалады. Қысқа мерзімді әсерлер де (соққанда) олар қатты денелерге ұқсайды, ол қатты соққанда кесектерге жарылады. Бірақ өте ұзақ әсер еткенде аморф денелер ағады. Төменгі температураларда аморф денелер қасиеттері жағынан қатты денелерге ұқсайды. Олардың аққыштығы жоқтың қасы.Бірақ температура жоғарлаған сайын біртіндеп жұмсара бастайды да, олардың қасиеттері бірте-бірте сұйықтардың қасиеттеріне көбірек жақындай түседі. Бұлай болу себебі температураның артуына қарай атомдардың бір тепе-теңдік қалыптан екіншіге секіру жиелене түседі. Кристалл денелерден аморф денелердің ерекшелігі – оларда белгілі балқу температурасы жоқ.
Қатты денелердің жылусыйымдылығы. Жылусыйымдылықтың классикалық теориясы. Дюлонг және Пти заңы.
П. Дюлонгпен біріге отыра бос денені суытқан уақыттағы өзгерістерді зерттеді, (1818) қыздырылған денелердің суыну жылдамдығының формуласын ашты және тәжірибелерге қажет катетометр құралын ойлап тапты.Газдардың жылу өткізгіштік әдісін зерттеді және қатты денелердің меншікті жылу сыйымдылығын, жылулық ұлғаюдың коэффициенттерін анықтау әдiстерiн ұсынды.
Катетометр - вертикаль бағытта орналасқан екі нүктенің арасындағы арақышықтықты дәл өлшеу үшін қолданылады.
Дюлонгтің ең басты ғылыми жетістігі 1819 жылы Пти екеуінің бірігіп анықтаған қатты дененің жылу сыйымдылық заңдылығы болып табылады. Осы заңдылыққа сәйкес қатты жай заттардың меншікті жылу сыйымдылығының туындысы түзілетін элементтердің атомдық массаларының сай келіп (жаңа өлшем бойынша орта есеппен 26 Дж·г−1·К−1) тең. Қазіргі уақытта бұл заңдылық Дюлонг – Пти заңдылығы атпен белгілі болып ауыр элементтердің атомдық массаларының мәніне жақын болды.
Бөлме температурасында қатты заттардың молярлық жылу сыйымдылығы 3R жақын болады.

R— универсал газ тұрақтысы. Қатты заттың кристалл торлары атомдардан тұрады, оның әрқайсысы үш бағытта гармониялық тербілісте болады, тордың құрылысын береді, бір - бірінен қатысынсыз әртүрлі бағытта тербеледі.
Қатты элементар бөлшектердің атомдық массасының туындысының меншікті жылу сыйымдылыққа қатынасы тұрақты өлшем болып табылады.Бұл заңдылық 13 қатты элементар денелер үшін расталды.Бірақ ол барлық химиктердің назарын аударды. Я.Берцелиус теориялық химияның жетістігі деп санап, осы заңдылық негізінде өзінің атомдық массалар кестесіне түзетулер енгізді. Сондықтан Дюлонг пен Пти ережесі химиялық атомистикада ең маңызды заңдылық болып қалды.П.Дюлонг және А.Пти (1819) ережесі бойынша элементтердің атомдық массаларын анықтау (молярлы массасын анықтау).Металдардың жылу сыйымдылықтарын зерттеу мақсатында Дюлонг және Пти төмендегідей ереже тұжырымдады:
Қатты күйіндегі жай заттардың меншікті жылу сыйымдылықтарының атомдық массаға (молярлы масса) көбейтіндісі тұрақты 26,0 кДж/ (моль*К) шамасына тең.
Көп заттардың меншікті жылу сыйымдылықтары тәжірибе жүзінде анықталады. Мұнан соң, сол заттың меншікті жылу сыйымдылығын 26,0 санына бөлу арқылы жуықтап молярлы массасын есептейді. Молярлы массаны сол заттың эквивалентінің молярлы массасына бөлу арқылы валенттілікті анықтайды. Шыққан сан бөлшек сан болса дөңгелектеу ережесіне сәйкес оны бүтінге айналдырады, өйткені валенттілік бүтін санмен анықталады.
Енді осы бүтін валенттілікті эквиваленттің молярлы массасына көбейту арқылы сол заттың дәл молярлы массасын анықтайды. Айтқандарымызды математика тілінде жазсақ, төмендегідей өрнек аламыз:
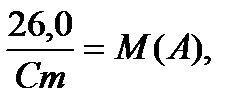

X≈ Z,
M(A) = Z *M (
Мұндағы Сm - меншікті жылу сыйымдылық,М(А) – А – затының молярлық массасы,Х- дөңгелектенетін сан,М(А) – затының эквивалентті молярлы массасы,Z –валенттілік.
Еске түсіре кететін жай, жекеленген атом, молекулалармен өлшеулер жүргізу мүмкін болмағандықтан біз тәжірибе жүзінде ылғи макроскопиялық деңгейде, яғни заттың белгілі бір мөлшерімен жұмыс істейміз. Осы себепті ылғи да молярлы шамалар анықталады.
Ал, өлшем бірлігін ескермегенде салыстырмалы атом, молекула массалары сан мәні жөнінен сол заттың молярлы атом, молекула массаларына тең.
Билет.
Энтропия түсінігі. Нернст теоремасы. Энтропияның физикалық мағынасы
Энтропия (грек. еntropіa – бұрылыс, айналу) – тұйық термодинамикалық жүйедегі өздігінен жүретін процестің өту бағытын сипаттайтын күй функциясы. Энтропияның күй функциясы екендігі термодинамиканың екінші бастамасында тұжырымдалады. Энтропия ұғымын термодинамикаға 1865 ж. Р.Клаузиус енгізген. Оны S арқылы белгілеген. Энтропия грек сөзі "бұрылыс, қайта оралу, түрлену" дегенді білдіреді.

1 суреттегі 1anb1 циклын қарастырайық. ТДның 2заңының жалпы өрнегінен,яғни  интегралын 2 интегралдың қосындысы ретінде алайық.
интегралын 2 интегралдың қосындысы ретінде алайық.
 (1) н-е циклдың қайтымды екенін ескерсек,
(1) н-е циклдың қайтымды екенін ескерсек,
 = -
= -  н-е
н-е  =
=  (2)
(2)
(2) интегралдың 1 және 2 күйлері арасындағы қайтымды жолына байланыссыз болуы осы интегралдың дененің қайсібір күй функциясының өзгерісін білдіретінін көрсетеді. Оны Клаузиус энтропия деп атады. Осы анықтама бойынша қайтымды проестегі энтропия өзгерісін былай жазамыз.
 (3) Өлшем бірлігі: [ Дж/К ]
(3) Өлшем бірлігі: [ Дж/К ]
Дененің әрбір күйі U ішкі энергияның мәнімен сипатталған сияқты S энтропияның белгілі бір мәнімен сипатталады.Энтропия да U сияқты толық дифференциал болады. S-тің абсолют мәнін есептеуге болушы еді, егер ол мән дененің қандай да бір күйі үшін белгілі болса. Мұндай мүмкіндік Нернст теоремасының негізінде пайда болды.
· Дененің S энтропиясының мәні абсолют температура нөлге жакындағанда нөлге тең болады.
Энтропияның физикалық мағынасы:
Карно циклының П.Ә.К ф-сынан шығатыны: көбірек жұмыс алу үшін қыздырғыштың температурасы мүмкіндігінше үлкен болу керек.Жұмыстың затқа қыздырғыш берген Q "+" деп есептегенбіз, демек Sте "+" болу керек- жұмыстық заттың энтропиясы да жоғары.
Егер Q-дың берілуі қыздырғыштың төмендеу температурасында өтсе, онда п.ә.к азаяды, ал энтропияның өсуі артады. Себебі формулады Т төменде тұр. Демек, энтропияның өсуі п.ә.к-тің кемуіне,яғни жұмыс көзі деп саналатын қыздырғыш құндылығының төмендеуіне әкеледі.Сондықтан энтропияны дене энергиясының құнсыздану мөлшері ретінде қарастыруға болады. Кейде мынадай тұжырым айтылады:энтропия дененің жұмысқа жарамай қалуының өлшемі, көрсеткіші.
6. Энтропияның қайтымсыз процестегі өзгерісі. Термодинамиканың негізгі теңдеуі.
Карноның қайтымды циклы, қандай да қайтымсызда- сондай жылулық кезінде және сондай жұмыста да, ПӘК-і өте үлкен болады; ол пайдалырақ, себебі T1' < T1 және T2' > T2 дене температурасының термиялық тепе-теңдігі жоқ кезінде өтеді. Механикалық тепе теңдіктің жоқ болуынан, өз кезегінде, қосымша үйкеліс шығынына әкеледі. Сонымен, формулаларға сай: (1 - q2/q1) < (1 - q2/q1) = 1 - T2/T1(штрихтар қайтымсыз жағдайларға жатады). Бұдан:q'1/q'2 < T1/T2 Карноның шексіз өте аз циклы үшін, теңдеуінің орнына dq'1/T1 < dq'2/T2, айналмалы қайтымсыз цикл үшін dq'2 теріс белгімен және Карноның элементарлы циклын, тағы да циклдарын бөлшектеу тәсілін қолдана отырып, тұйық пішіні бойынша интегралданғаннан кейін табамыз: ʃ dq' /T < 0. Қайтымсық және қайтымды циклдарды жалпы жағдайы үшін: ʃ dQ/T < 0. Мұндағы теңдік таңбасы, бұрыннан белгілі, қайтымды циклға және Клаузиус теңдңгңне жатады. Екі өтпелі 1 —>2 және 2 —> 1 қалай болса солай алынған, айналмалы циклды қарастырамыз және солай деп 2 —> 1 өтуі шексіз өте аз қайтымды процестерден, ал 1 —> 2 өтуі қайтымсыздан тұрады. Екеуін бірге алғандағы өтуі, қайтымсыз айналмалы процесті құрайды. Себебі, оның бөлігі қайтымсыз.Егер, формула қайтымды өтуіне арналған деп қабылдасақ, онда теңсіздік мына түрінде жазылады:∫12dq'/T+S1-S2<0. Бұдан мынадай қорытынды шығады: ∫12dq'/T+S1-S2немесе ds > dq' / Т. Формула қайтымсыз процесске арналған, жылудинамикасының екінші заңының теңдеуі болып есептелінеді. Сонымен, жылудинамикасының екінші заңының мазмұны тәжірибе фактысына негізделген және қайтымсыз процессте өтеді. Бұл заңды, осы түрінде алғаш рет Клаузиус тұжырымдаған: жылулық өз өзінен дененің аз температуралығынан басқа дененің үлкен температурасына(компенсациясыз) еш уақытта өтпейді. Клаузиус өзінің пастулатында амалсыз компенсация ретінде қабылдап, ол кездегі жұмыс шығынының жылулыққа алмасуын дәлелдеді.
Термодинамиканың негізгі теңдеуі
Қайтымды пр. үшін dS≥∫12 d'Q/T формуласындағы d'Q шамасын Т.Д 1 заңына ауыстырамыз: dS=(dU+PdV)/T. Бұл ТДның негізгі теңдеуі. Мұнда ТД бірінші және екінші формулалары біріктірілген. Оны идеал газдың S өзгерісін есептеу үшін қолданайық: dU=CvdT және P=RT/V болғандықтан dS=CVdT/T+R dV/V (2). интегралдасақ: S=CVlnT+RlnV+S0 S0 –бұл интегралдау тұрақтысы. Егер ид. газдың 1 моль T1 темп-да V1 көлемді алып, қайтымды процеспен T2 ж/е V2 күйге көшсе, онда (2) формуланы интегралдар Sтің өзгерісін табамыз. S2-S1=CVln T2/ T1 +Rln V2/ V1---бұл жүйе 1 күйден 2ши күйге қайтымды процеспен өткендегі Sэнтропиясының өзгерісі осы күйлердегі энтропия шамаларының айырмасына тең және бұл көшу қандай аралық күйлермен өткендігіне байланыссыз болады. Егер Т өзгерісі V=const кезінде болса, онда энтропияның өзгерісі мынаған тең: S2-S1=CVln T2/ T1
Билет.
Энтропияның адиабаталық процесте, жылуалмасуда және идеал газдың бос кеңістікке ұлғайғанда өзгеруі.
8. Карно теоремасы. Температуралардың термодинамикалық шкаласы.
Карно теоремасы
С. Карно термодинамикалық циклға жататын идеал жылу машинасының жобасын ұсынған. Карно циклі деп аталған бұл дөңгелек процесс 2 тепе – тең изотермалық, адиабаталық процестерден құралады. Машинада жылу өткізгіштікке, үйкеліске және т.б. кететін шығын болмайды. Цикл жүзеге асу үшін жұмыстық затқа изотермиялы ұлғайғанда жылу беретін қыздырғыш және изотермиялы сығылғанда жылу алатын суытқыш болуы қажет.
Температуралары Т1 және Т2 қыздырғыш пен суытқыш алайық. Жұмыстық зат ретінде ид. газ алынады. Жұмыстық заттың қыздырғыштан алған жылу мөлшерін Q1, ал суытқышқа берген жылуын Q2 деп белгілінеді. Циклде жасалған жұмыс А барлық жағдайда оң, яғни заттың ұлғаюы кезінде А1>0, ал оны сығатын сыртқы күш А2<0. Енді жұмыстық зат ретінде 1 моль ид.газ алып Карноның идеал жылу маш-ның жұмыс істеу принципін зерттелік.
1. Дөңгелек процесс. Бастапқыда газ көлемі V1 ден V2-ге дейін изотермалы ұлғайта отырып 1-күйден 2-күйге өтті. Бұл кезде алған жылу  түгелдей ұлғаю жұмысын жасауға жұмсалады, яғни,
түгелдей ұлғаю жұмысын жасауға жұмсалады, яғни,  .
.
2. Зат қыздырғыштан бөлектеніп адиабаталық түрде ұлғаяды және 2-күйден 3-күйге
ауысады. Онда температура Т1-ден Т2-ге дейін кемиді. Себебі, газ ішкі энергияның есебінен адиабаталы үлғая отырып жұмыс жасайды.
 .
.
3. Сыртқы күш әсерінен изотермалы түрде сығылып 3-күйден 4-күйге ауысады, сонда газды V3 тен V4 көлем1ге дейін сығуға жұмсалатын жұмыс  . Бұл жұмыс суытқышқа беретін жылу мөлшеріне, яғни Q2-ге тең.
. Бұл жұмыс суытқышқа беретін жылу мөлшеріне, яғни Q2-ге тең.
4. Газды адиабаталық түрде сығу арқылы 4-күйден 1-күйге ауысады. Жұмыс:
 . Мұнда А4=Q4.
. Мұнда А4=Q4.
Карно циклінде жасалған жалпы жұмыс осы 4 жұмыстың қосындысына тең:
 .
.
Адиабаталық ұлғаю және сығылу процестері үшін Пуассон теңдеуі былай жазылады:
 және
және 
Бұдан  ,болып Карно циклінде атқарылған пайдалы жұмыс:
,болып Карно циклінде атқарылған пайдалы жұмыс:

Осы формуладан Карно циклімен жұмыс жасайтын идеал жылу машинасының П.Ә.К анықталады: 
Карно циклінің П.Ә.К-і тек абсолют температуралардың қатынасымен анықталады. Қайтымды Карно циклі үшін 

Бұл өрнек термодинамиканың екінші бастамасының тағы бір анықтамасы болып табылады: «Идеал жылу машинасының ПӘК-і қыздырғыш пен суытқыштың температураларымен ғана анықталады». Қайтымсыз процес үшін барлық жағдайда:
 , олай болса қатынас жалпы түрде былай жазылады:
, олай болса қатынас жалпы түрде былай жазылады: 
мұндағы теңсіздік қайтымсыз, ал теңдік қайтымды процестерге сәйкес келеді. Демек, Карно циклінің ПӘК-і берілген температуралар интервалында басқа циклдармен салыстырғанда ең жоғары. Бұл Карноның бірінші теоремасы.
Екінші теорема былай тұжырымдалады: «Карноның идеал циклінің ПӘК-і жұмыстық дененің тегіне байланысты емес».
Температуралардың термодинамикалық шкаласы.
Карно теоремаларының негізінде температураның термодинамикалық шкаласын жасауға болады. Бұл шкала термометрлік денеге де, температуралық параметрге де тәуелсіз.
PV диаграммада изотермалар және оны қиятын адиабаталар жүйесі жүргізілген. Көрші изотермалар мен адиабаталардың арасындағы 1,2,3 фигуралар Карно циклы екендігі айқын. Осы циклды кез келген жұмыстық дене үшін қайтымды жолмен жүзеге асырайық. Карно циклымен жұмыс істейтін идеал жылу машинасынң ПӘК-нің өрнегінен бірінші цикл үшін Т1 және Т2 температуралар аралығында  қатынасы орындалады. Циклдың қайтымдылығынан Т2,Т3 температуралар аралығы үшін
қатынасы орындалады. Циклдың қайтымдылығынан Т2,Т3 температуралар аралығы үшін  , ал Т3, Т4 температуралары интервалы үшін
, ал Т3, Т4 температуралары интервалы үшін 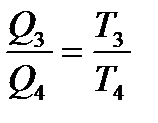
қатынастары орындалады. Осылардан Т1: Т2: Т3= Q1: Q2: Q3 ... сондықтан  қатынасы термодинамикалық шкала бойынша абсолют температураның анықтамасы болып табылады. Бұны анықтаған ағ. Ғалымы Кельвин, сондықтан ол Келвин шкаласы деп аталады.
қатынасы термодинамикалық шкала бойынша абсолют температураның анықтамасы болып табылады. Бұны анықтаған ағ. Ғалымы Кельвин, сондықтан ол Келвин шкаласы деп аталады.
Халқаралық бірліктер жүйесінде температураның негізгі бірлігі ретінде абсолюттік шкаламен саналған градус алынады. Оның аты Кельвин (К).Кельвин судың үштік нүктесінің термодинамикалық температурасының  бөлігі. Бұл анықтама ПӘК-тің жұмыстық денеге байланыссыз Карноның қайтымды циклын қарастыру арқылы алынғандақтан, заттың қасиетіне байланыссыз. Яғни, термодинамикалық шкала термометрлік денеге байланыссыз.
бөлігі. Бұл анықтама ПӘК-тің жұмыстық денеге байланыссыз Карноның қайтымды циклын қарастыру арқылы алынғандақтан, заттың қасиетіне байланыссыз. Яғни, термодинамикалық шкала термометрлік денеге байланыссыз.
Билет.
Идеал газдың ішкі энергиясы. Жұмыс және жылу. Термодинамикалық жұмыстың геометриялық түсініктемесі
Идеал газ деп газ молекулаларының материалдық нүкте ретінде қарастыруға болатын және олардың бір бірімен әсерлесуі жоқ, тек қана серпімді соқтығыспен әсерлесетін газды айтамыз. Дененің ішкі энергиясы – бұл молекулалардың жылулық қозғалысының кинетикалық энергиясы мен олардың өзара әсерлесуінің потенциалдық энергиясының жиынтығы.Идеал газда молекулааралық өзара әсерлесу күштері болмайтындықтан, оның ішкі энергиясы тек молекулалардың хаостық қозғалысының кинетикалық энергияларынан ғана құралады. Идеал газдың бір моль мөлшері үшін оның ішкі энергиясы:
 ,
,
ал газдың кез-келген массасы үшін
 .
.
Термодинамикада қозғалыстағы ортаның аз бөлшектерiнiң бiр-бiрiне қатысты орын ауыстыруы ғана қарастырылады. Нәтижесiнде дене көлемi, оның iшкi энергиясы өзгередi. Дене жылдамдығы тұтасымен алғанда нөлге тең болып қалады. Жұмыс классикалық механикадағы сияқты анықталады, бiрақ ол дененiң кинетикалық энергисының өзгеруiне емес, оның iшкi энергиясының өзгеруiне тең болады. Мысалы, газдардың сығылуы кезiнде поршень өзiнiң механикалық энергиясының бiр бөлiгiн газдарға бергендiктен, молекулалардың кинетикалық энергиясы ұлғаяды, газ қызады. Керiсiнше, егер газ ұлғайса, онда алыстаған поршенмен соқтығысқаннан кейiн молекулалардың жылдамдығы азайып, газ суиды
. Жұмысты есептеу. Қозғалмалы ортаның көлемi өзгергендегi iстелген жұмыс мынаған тең болады
А ′ = p · (V2-V1) = p · ΔV. (3.1)

|
| 3.1-сурет |

|
| 3.2-сурет |
Ұлғаю кезiнде (V2 > V1) газ оң жұмыс жасайды: А′ >0. Сығылу кезiнде V2 < V1, сондықтан оның жұмысы терiс болады: А′ <0. Керiсiнше, газ сығылған кездегi сыртқы күштердiң жұмысы оң болады да, газ қыза бастайды. Ұлғаю кезiнде сыртқы күштердiң жұмысы терiс болады – газ суиды.
Тұрақты қысым жағдайында, газдың жұмысы геометриялық тұрғыдан түсiндiргенде 3.1.–суретiнде келтiрiлген (P-V) графигiндегi V1АВV2 тiк төртбұрышының ауданына дәлме-дәл тең екендiгiн оңай көруге болады. Жалпы жағдайда газ қысымы көлемге байланысты функция болып табылады. Бiрақ, газ жұмысы бұрынғысынша сандық түрде бастапқы және соңғы күйлердегi p1 және p2 қысымдарына тең AV1 және ВV2 кесiндiлерiмен және P -ның V -ға байланысты графигiмен шектелген фигураның ауданына тең болады(3.2-сурет).
Жылу дегеніміз бір-біріне түйіскен денелердегі молекулаларың өзара соқтығысу (қақтығысу) арқылы, яғни система ішінде жылу алмасу жолымен энергияны беру, жеткізу түрі. Жылудын, бағытын және өзара берілуін, қозғалысын температура көрсетеді.
Не нашли, что искали? Воспользуйтесь поиском: