И ДОСТАТОЧНЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ

ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ. НЕОБХОДИМЫЕ

Рассмотрим общую математическую постановку экстремальных задач, сформулируем условия существования и признаки оптимальности их решений.

Предварительно напомним, что латинское слово extremum оз­начает «крайнее». Оно в математике имеет два конкретных зна­чения: maximum (сокращенно max) — наибольшее и minimum (со­кращенно min) — наименьшее. В таком понимании extremum имеет более узкий смысл, чем optimum, переводимый с латинского как «наилучшее».

Пусть дана функция f: Х→ R¹, где Х 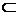Rⁿ. Говорят, что в точке х* 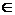X достигается максимальное (минимальное) значение функции f, если выполнено неравенство f (х*) ≥ f (х) (f (х*) ≤ f (х)) для всех х 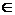X.

Точка х*, в которой достигается максимум (минимум), назы­вается точкой максимума (минимума) функции f.

Задача нахождения максимального или минимального значе­ния заданной функции на заданном множестве называется экст­ремальной задачей.

Как видим, имеется два вида экстремальных задач — задача на максимум и задача на минимум. Символически они записыва­ются так:

. (2.5)

В (2.5) функция f называется целевой функцией, а X— множе­ством допустимых решений. Оптимальным решением задач (2.5) называется пара (x*,f (x^*)), где х * — точка максимума (минимума), а f (х *) — значение функции f в этой точке, т. е. ее максимальное (минимальное) значение на множестве X.

Решить задачи (2.5) это значит либо найти оптимальное ре­шение, либо убедиться, что оптимального решения не суще­ствует.

Решение задач (2.5) требует разрешения трех проблем:

1) проблемы существования оптимального решения;

2) проблемы установления необходимых и достаточных при­знаков оптимальности (т. е. характерных свойств, присущих точ­кам максимума и минимума);

3) проблемы численного вычисления оптимальных решений.

В экономической практике встречаются случаи, когда постав­ленная цель не может быть достигнута ввиду тех или иных объек­тивных причин. Подобно этому, оптимальные решения задач (2.5) существуют не всегда.

Сформулируем условия, при которых такие решения суще­ствуют.

В задачах (2.5) применяются экстремальные точки двух ви­дов: локальный максимум (минимум) и глобальный максимум (минимум). Точка х₀ 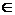X называется точкой локального максиму­ма (минимума), если f (х °) ≥ f (х) (f (х °) ≤ f (х) для всех х 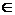O_ε (х °), где О_ε (х °) — ε-окрестность точки х°. Точка х₀ 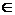X называется точкой глобального максимума (минимума), если эти неравенства выполняются для всех х 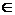X.

Достаточное условие существования оптимальных решений задач (2.5) содержится в следующем утверждении.

Теорема (Вейерштрасса). Для того чтобы в задачах (2.5) суще­ствовала точка глобального максимума (минимума), достаточно, чтобы допустимое множество Х было компактно в Rⁿ, а целевая функция f непрерывна на X.

Ввиду сложности проверки ограниченности множества X на практике часто применяется следствие из этой теоремы.

Следствие (теоремы Вейерштрасса). Если функция f непре­рывна на Rⁿ и

то f достигает своего глобального минимума (максимума) в лю­бом замкнутом подмножестве X пространства Rⁿ.

Необходимые и достаточные признаки оптимальности игра­ют важную роль в решении задач (2.5). Необходимые признаки всегда «сопровождают» оптимальное решение, потому с их по­мощью можно вычислить точки, подозрительные на экстремум. Выполнение достаточных признаков для какой-либо допустимой точки х 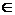X гарантирует оптимальность этой точки. Поэтому до­статочные признаки можно использовать для нахождения опти­мального решения из совокупности допустимых точек, удовлет­воряющих необходимым признакам.

Признаки оптимальности приведем в случае, когда в (2.5) Х≡ Rⁿ. В этом случае задачи (2.5) принимают вид

(2.6)

и называются задачами безусловной оптимизации.

Для того чтобы точка х ⁰ 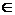Rⁿ была точкой локального экстре­мума в задачах (2.6), необходимо, чтобы

. (2.7)

Это есть необходимый признак оптимизации I порядка. Все точ­ки х °, удовлетворяющие условию (2.7), называются стационарны­ми точками (точки, подозрительные на экстремум).

Среди стационарных могут быть точки, не являющиеся точ­ками экстремума.

Пример 2.4. f (х) = х³ → max (min), х 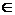R¹

Уравнение (2.7) имеет вид 3 х ² = 0. Отсюда получим стацио­нарную точку х ° = 0. Построив график функции f, можно убе­диться, что точка х ° = 0 не является точкой экстремума (это есть точка перегиба графика f).

Следующие примеры показывают, что с помощью условия (2.7) можно показать и отсутствие решения в задачах (2.6).

Пример 2.5. f (х) = х ₁² + х ₂² – 2 х ₁ х ₂ + х ₁ → max (min), х 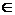R ². Уравнение (2.7) имеет вид

2 х ₁ – 2 х ₂ +1 = 0,

–2 x ₁ + 2 x ₂ =0.

Эта система несовместна, т. е. нет ни одной стационарной точки, и наша задача не имеет решения.

Пример 2.6. f (х) = х ₁² – х ₂² – 2 х ₁ х ₂ + х ₁ → min, х 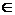R ². Стационарной является единственная точка х ⁰ = (—1/4, —1/4). Однако она не является точкой минимума, так как, например, для точки 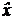= (0, 1) имеем f (х ⁰) = –1/8 >–1 = .

Условие (2.7) выполняется как для точки максимума, так и для точки минимума. Поэтому для выяснения характера экстре­мума стационарных точек к ним применяют более сложные не­обходимые признаки оптимальности II Порядка.

Пусть в (2.6) функция дважды дифференцируема в точке х ⁰. Для того чтобы х ⁰ была точкой локального максимума (мини­мума) в задаче (2.6), необходимо, чтобы

и , (2.8)

для всех α 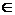Rⁿ. Здесь 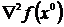— матрица Гессе функции f в точке х ⁰, а — скалярное произведение.

Однако при выполнении условий (2.8) точка х ⁰ не обязатель­но будет точкой локального экстремума. Для этого нужно, чтобы она удовлетворяла и достаточным признакам.

Для того чтобы х ⁰ была точкой локального максимума (мини­мума) в задаче (2.6), достаточно, чтобы

и , (2.9)

для всех α 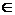Rⁿ.

Условия (2.8) и (2.9) связаны с вогнутостью и выпуклостью функции f. Известно, что дважды дифференцируемая на выпук­лом множестве X функция f вогнута (выпукла) тогда и только тогда, когда для любых векторов х ⁰ 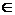Rⁿ и α 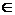Rⁿ справедливо условие (2.8). В случае же выполнения условия (2.9) говорят о строгой вогнутости (выпуклости) функции f.

С другой стороны, условие (2.8) является признаком отрица­тельной (положительной) полуопределенности матрицы Гессе. Напомним, что матрица будет отрицательно полуопределенной в точке х ⁰, если

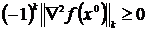, (2.10)

для всех k =1,..., п. Здесь символом обозначен минор k- гопорядка матрицы :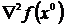

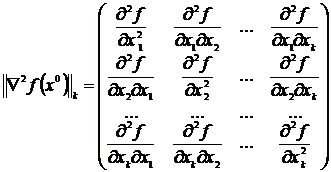
где |.| — определитель порядка k х k, вычисляемый в точке х ⁰.

Условие (2.10) означает, что знаки миноров чередуются, причем первый минор .

Матрица будет положительно полуопределена тогда и только тогда, когда все миноры матрицы Гессе будут неотрицательны

. (2.11)

Если в (2.10) и (2.11) неравенства строгие, то получаем необходимое и достаточное условие отрицательной (2.10) и положительной (2.11) опреде­ленности матрицы Гессе в точке х ⁰. Условия (2.10) и (2.11) называется критерием Сильвестра для знакоопределенных матриц.

Известно, что если матрица Гессе в точке х ⁰ положительно определена, то точка х ⁰ является точкой локального минимума. Если же матрица Гессе в точке х ⁰ отрицательно определена, то точка х ⁰ является точкой локального максимума.

Поскольку условия (2.8) и (2.9) трудно проверяемы, то при проверке необходимых условий оптимальности в задачах (2.6) применяют критерий Сильвестра.

Следовательно, при помощи условий (2.7)—(2.9) можно пред­ложить следующий алгоритм решения задач (2.6):

1) вычислить все стационарные точки (найти все решения уравнения (2.7));

2) выяснить характер экстремума стационарных точек (с ис­пользованием условий (2.8), (2.9)), для чего применить критерий Сильвестра;

3) среди всех точек локального максимума (минимума) найти точки глобального максимума (минимума), сравнивая значения функции/в этих точках.

Пример 2.7. f(х) = х₁⁴ + х₂⁴ -(х₁ + х₂)² → max(min), x 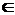R².

1. Уравнение (2.7) имеет вид

Решая эту систему (третьего порядка), находим (три) стационар­ные точки: х ⁰= (0, 0), х ⁰⁰ = (1, 1), х ⁰⁰⁰ = (–1, –1).

2. Выясним характер экстремума, для чего сначала вычислим все главные миноры матрицы Гессе:

, .

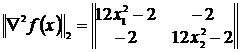Для точки х ⁰= (0, 0) имеем

,

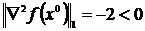Видно, что критерий для локального минимума не выполнен. Однако 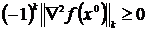, k = 1, 2, т. е. матрица отрица­тельна, полуопределена и, следовательно, для точки х ⁰выполне­но необходимое условие локального максимума. Так как это лишь необходимое условие, в точке х ⁰ может и не быть локального максимума. Нужно ее дополнительно исследовать. Рассматривая знак производной функции f вблизи х ⁰, т. е. в точках х ⁰ – ε и х ⁰ + ε, ε > 0, можно убедиться в том, что х ⁰ не является точкой (локального) максимума.h

Для точки х ⁰⁰ = (1,1) имеем

,

Следовательно, матрица положительно определена, т. е. для точки х ⁰⁰выполнено достаточное условие локального минимума.

Легко установить, что 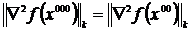, k =1,2, т. е. х ⁰⁰⁰ = (–1, –1) также является точкой локального минимума.

3. Найдем точки глобального минимума: f (x ⁰⁰) = –2, f (x ⁰⁰⁰) = –2, то есть точки x ⁰⁰ и x ⁰⁰⁰ являются точками глобального минимума (поскольку было установлено, что минимум целевой функции существует).

Не нашли, что искали? Воспользуйтесь поиском: