Задачи линейного программирования

Стандартная задача линейного программирования состоит из трех частей:

* целевой функции (на максимум или минимум) - формула (7.3.1);

* основных ограничений (³, £, =) - формула (7.3.2);

* ограничения неотрицательности переменных (есть, нет) - формула (7.3.3).

, (7.3.1)

, i = 1,..., m, (7.3.2)

x_j ³ 0,j =1,..., n. (7.3.3)

Алгоритм решения задач линейного программирования требует приведения их постановки в канонический вид, когда целевая функция стремится к максимуму (если она стремилась к минимуму, то функцию надо умножить на - 1, она станет стремиться к максимуму), основные ограничения имеют вид равенства (для приведения к равенствам в случае знака £ надо в правую часть каждого такого k - го неравенства добавить искусственную переменную u_k ³ 0, а в случае знака ³, u_k ³ 0 надо отнять из правой части основных ограничений), присутствуют ограничения неотрицательности переменных (если их нет для некоей переменной x_k, то их можно ввести путем замены всех вхождений этой переменной комбинацией x¹_k - x²_k = x_k, где x¹_k ³ 0 и x²_k ³ 0 ). При этом для решения задачи линейного программирования необходимо иметь базис, т.е. набор переменных x_i, количеством, равным числу основных ограничений, причем чтобы каждая из этих переменных присутствовала лишь в одном основном ограничении и имела свой множитель a_ij = 1. Если таких переменных нет, то они искусственно добавляются в основные ограничения для получения индексов x_m+1, x_m+2 и т.д. Считается при этом, что они удовлетворяют условиям неотрицательности переменных. Заметим, что если базисные переменные (все) образуются в результате приведения задачи к каноническому виду, то целевая функция задачи остается без изменений, а если переменные добавляются искусственно к основным ограничениям, имеющим вид равенств, то из целевой функции вычитается их сумма, умноженная на M, т.е. 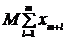(так называемый модифицированный симплекс-метод). Мы не будем рассматривать задачи, относящиеся к модифицированному симплекс-методу. Для практической работы по нахождению решения задачи линейного программирования (по варианту простого симплекс-метода) будут использоваться алгоритм итерационного (многошагового) процесса нахождения решения и два типа оперативных оценок, позволяющих делать переходы от одного шага к другому, а также показывающих, когда итерационный процесс остановится и результат будет найден.

Первая оценка - это дельта-оценка, для переменной x_j она имеет вид

. (7.3.4)

Здесь выражение i Î B означает, что в качестве коэффициентов целевой функции, представленных в сумме выражения (7.3.4), используются коэффициенты переменных, входящих в базис на данном шаге итерационного процесса. Переменными a_ij являются множители матрицы коэффициентов A при основных ограничениях, рассчитанные на данном шаге итерационного процесса. Дельта-оценки рассчитываются по всем переменным x_i, имеющимся в задаче. Следует отметить, что дельта-оценки базисных переменных равны нулю. После нахождения дельта-оценок из них выбирается наибольшая по модулю отрицательная оценка, переменная x_k, ей соответствующая будет вводиться в базис.

Другой важной оценкой является тетта-оценка, имеющая вид

. (7.3.5)

То есть по номеру k, найденному по дельта-оценке, мы получаем выход на переменную x_k, и элементы столбца X^B делим на соответствующие (только положительные) элементы столбца матрицы A, соответствующего переменной x_k. Из полученных результатов выбираем минимальный, он и будет тетта-оценкой, а i -й элемент столбца X^B, лежащий в одной строке с тетта-оценкой, будет выводиться из базиса, заменяясь элементом x_k, полученным по дельта-оценке. Для осуществления такой замены нужно в i - ой строке k -ого столбца матрицы A сделать единицу, а в остальных элементах k-го столбца сделать нули. Такое преобразование и будет одним шагом итерационного процесса.

Для осуществления такого преобразования используется метод Гаусса. В соответствии с ним i -я строка всей матрицы A, а также i -ый элемент столбца X^B делятся на a_ik (получаем единицу в i -ой строке вводимого в базис элемента). Затем, вся i -ая строка (если i не единица), а также i -ый элемент X^B умножаются на элемент (-a_1k). После этого производится поэлементное суммирование чисел в соответствующих столбцах 1-ой и i - ой строк, суммируются также X^B₁ и (‑a_1k) ЧX^B_i. Аналогичные действия производятся для всех остальных строк кроме i -ой (базисной) строки.

В результате получается, что в i -ой строке k -го элемента стоит 1, а во всех остальных его строках находится 0. Таким образом осуществляется шаг итерационного алгоритма. Шаги алгоритма симплекс-метода продолжаются до тех пор, пока не будет получен один из следующих результатов:

· все небазисные дельта-оценки больше нуля - найдено решение задачи линейного программирования, оно представляет собой вектор компонент x_i, значения которых либо равны нулю, либо равны элементам столбца X^B, такие компоненты стоят на базисных местах (скажем, если базис образуют переменные x₂, x₄, x₅, то ненулевые компоненты стоят в векторе решения задачи линейного программирования на 2-ом, 4-ом и 5-ом местах);

· имеются небазисные дельта-оценки, равные нулю, тогда делается вывод о том, что задача линейного программирования имеет бесчисленное множество решений (представляемое лучом или отрезком). Подробно рассматривать случаи такого типа, а также отличия между решениями в виде луча и отрезка мы не будем;

· возможен вариант получения столбца отрицательных элементов на отрицательной рассчитанной дельта-оценке, в такой ситуации нельзя вычислить тетта-оценки. В этом случае делается вывод, что система ограничений задачи линейного программирования несовместна, следовательно, задача линейного программирования не имеет решения.

Решение задачи линейного программирования, если оно единственное, следует записывать в виде X* = (...,...,...) - вектора решения и значения целевой функции в точке решения L*(X*). В других случаях (много или отсутствует решение) следует словесно описать полученную ситуацию: если решение задачи линейного программирования не будет получено в течение 10-12 итераций симплекс-метода, то следует написать, что решение отсутствует в связи с неограниченностью функции цели.

Для практического решения задачи линейного программирования симплекс-методом удобно пользоваться таблицей.

Таблица 7.3.1

B	CB	XB	A1	...	An	q
Базисные компоненты	Целевые коэффициенты базиса	Правые части ограничений
D			D1		Dn

Математика – единственный совершенный метод,
позволяющий провести самого себя за нос.

А. Эйнштейн

Не нашли, что искали? Воспользуйтесь поиском: