Задачи нелинейного программирования

Рассмотрим численные методы решений задач нелинейного программирования. Следует отметить, что не существует универсального метода, способного помочь в решении любых задач НП. Поэтому рассмотрим наиболее распространенные. Но вначале введем понятие унимодальной функции.

Унимодальной функцией на [ a; b ] называется функция, имеющая на этом отрезке единственную точку глобального минимума. При этом слева от этой точки функция является строго убывающей, с справа - строго возрастающей.

Унимодальная функция имеет важное свойство. Если , то , если , то .

Рассмотрим задачу оптимизации для унимодальной функции на отрезке [ a; b ]. В принципе простейшим методом решения является методика перебора всех значений целевой функции на заданном интервале. В условиях применения средств вычислительной техники такая идея представляется не очень-то и абсурдной, но все-таки достаточно трудоемкой. Поэтому, если идею перебора значений целевой функции в целом оставить, но уточнить алгоритм выбора точек, в которых необходимо осуществить вычисление целевой функции, то можно получить достаточно эффективный метод решения оптимизационных задач. Одним из таких алгоритмов и является метод «золотого сечения». Сущность алгоритма заключается в следующем: значение целевой функции вычисляется в произвольных точках x₁ и x₂. Возможно f(x₁)=f(x₂) или f(x₁)>f(x₂). Так как функция унимодальна, то согласно ее свойству экстремум ее будет находиться на отрезке [ a; x₂ ], а во втором случае [ x₁; b]. Таким образом, произошло сужение интервала поиска экстремума и следующую точку необходимо брать внутри укороченного интервала.

Выбор точек x₁ и x₂ должен осуществляться по определенному алгоритму, то есть они должны делить рассматриваемый интервал в пропорции, называемой золотым сечением отрезка.

Золотым сечением отрезка называется точка, отстоящая на расстоянии длины от одного из ее концов. Опишем алгоритм.

ШАГ 0. Вычисляются координаты точек, осуществляющих золотое сечение исходного отрезка:

Вычисляются значения целевой функции в этих точках, то есть и .

ШАГ k (k =1). Сравним значения. Если , то полагаем , и, используя эти числа, вычисляем координату симметричной точки (слева от имеющейся) и значение f (y_k).

Если же 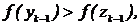то следует принять и вычисляем координату симметричной точки (справа от имеющейся) и значение f (z_k).

Итерация продолжается до тех пор, пока длина k =1-го отрезка не достигнет заранее заданной точности вычислений. Затем выбирают наименьшее из чисел и . Это и будет приближенный минимум.

На 0-ом шаге значение целевой функции вычисляется дважды, а на каждом последующем только по одному разу.

Другим методом минимизации, обладающим лучшей сходимостью при одинаковом числе шагов по сравнению с методом «золотого сечения», является метод Фибоначчи.

На нулевом шаге координаты точек вычисляются по формулам:

где – число Фибоначчи, определяемое по реккурентной формуле

Запишем первые десять чисел Фибоначчи:

.

Дальнейшая методика вычислений осуществляется так же, как и в методе золотого сечения. Отличие заключается в том, что не надо вычислять величину интервала , так как при k=n- 1 процесс заканчивается и принимается за приближенное значение экстремума.

Для построения итерационного процесса служат следующие формулы

В остальном алгоритм полностью подчиняется методу золотого сечения.

На практике часто задается точность вычислений ξ, а не число шагов. В этом случае для определения числа шагов используют соотношение

.

При метод Фибоначчи совпадает с методом золотого сечения.

При решении задач с помощью методов золотого сечения и Фибоначчи важным условием является свойство унимодальности целевой функции. Если же оно не соблюдается, то реализация этих методов приведет к отысканию локального экстремума, который может сколь угодно сильно отличаться от глобального экстремума.

Другим методом решения задач нелинейного программирования являются методы спуска.

Сущность методов спуска заключается в построении последовательности точек , монотонно уменьшающих значение целевой функции

такая последовательность получила называние минимизирующей.

Для построения минимизирующей последовательности берется точка x , выбирается направление спуска и длина шага вдоль этого направления Cледующая точка, получается в результате вычислений по формуле

.

Различные методы спуска различаются методом выбора шага и направления спуска . При этом существует следующая классификация. Если для определения параметров спуска требуется вычисление только значений целевой функции, то такие методы называют методами нулевого порядка. Если кроме вычисления значений целевой функции требуется вычисление еще и ее первых производных, то такие методы получили название методов первого порядка. Если же необходимо вычислить и вторые производные, то это методы второго порядка.

Согласно этому методу направление спуска выбирается параллельным координатным осям. Сначала производится спуск вдоль оси ОХ₁, затем - вдоль оси ОХ₂ и т.д.

Алгоритм строится следующим образом: пусть х₀ - точка начального приближения, тогда вычисляют следующее значение:

,

где - единичный орт, то есть вектор единичной длины, у которого все координаты, кроме 1, равны 0. Вычисляется значение целевой функции в этой точке и проверяется неравенство

.

Если это неравенство выполняется, то вдоль оси ОХ₁ значение функции уменьшилось и поэтому полагают , .

Если неравенство не выполняется, то проверяют неравенство

,

и если оно выполняется, то в качестве следующего приближения принимают .

Если и в этом случае неравенство будет невыполнимо, тогда считают и . Второй шаг производят вдоль координатной линии ОХ₂, и проверяют справедливость неравенства

.

Если оно выполняется, то полагают

Если неравенство не выполняется, то проверяют выполнение неравенства . В этом случае, если оно справедливо, тогда принимают . Если несправедливо, то , . Таким образом, происходит перебор всех n координат. На этом 1-ая операция закончена. Получена некоторая точка х ₁;если , то аналогично осуществляют вторую операцию. Если же , то величину шага a следует уменьшить, взяв, например, , и в следующей итерации использовать новое значение шага.

Вычисления продолжают до тех пор, пока не будет достигнута некоторая наперед заданная точность счета, проверяемая с помощью неравенств .

Сходимость метода достигается для выпуклых и непрерывно дифференцируемых функций.

Остается открытым вопрос о выборе начального приближения х₀ для решения исходной задачи, так как неудачный выбор может привести к расходящемуся процессу.

Рассмотренный метод относится к методам нулевого порядка.

Данный метод может быть использован и в задачах с ограничениями на значение x_i. В этом случае не для каждой итерации требуется проверять условия допустимости новой точки х_k+1. Если хотя бы одно из условий нарушается, то значение координаты остается прежним.

Если найти градиент функции f (x) в точке х ₀, то антиградиентом будет называться функция - . Антиградиент показывает направление уменьшения функции f (x). Это свойство послужило основой градиентных методов. Согласно этим методам на k -итерации последующее приближение к решению задачи вычисляют по формуле:

Методы отличаются способом выбора множителя a_k. Если a_k достаточно мало, то при этом наверняка обеспечивается выполнение неравенства , но число итерацией может быть очень велико. С другой стороны, при больших значениях a_k неравенство может и не выполняться.

Наиболее простой способ выбора a_k - это положить его одинаковым для всех итераций. При этом если неравенство будет нарушаться, то для данной итерации a уменьшается до тех пор пока, указанное неравенство не будет справедливым.

Предпочитай убыток позорной прибыли: первое
огорчит один раз, второе будет огорчать всегда.

Хилон

Не нашли, что искали? Воспользуйтесь поиском: