
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Классификация задач оптимизации
Рассмотрим систему (причем совершенно не важен характер этой системы, ее назначение, это может быть производственная система, финансовая, социальная или механическая), состояние которой описывается некоторым набором изменяемых параметров:  , а качество функционирования оценивается некоторой функцией от этих параметров состояния, называемой целевой функцией. Возникает вполне естественное желание добиться такой комбинации параметров состояния
, а качество функционирования оценивается некоторой функцией от этих параметров состояния, называемой целевой функцией. Возникает вполне естественное желание добиться такой комбинации параметров состояния 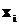 , чтобы качество функционирования системы было бы наилучшим, то есть целевая функция должна принимать максимальное или минимальное значение. В этом случае возникает задача оптимизации, которую можно записать в общем виде следующим образом:
, чтобы качество функционирования системы было бы наилучшим, то есть целевая функция должна принимать максимальное или минимальное значение. В этом случае возникает задача оптимизации, которую можно записать в общем виде следующим образом:
 (7.1.1)
(7.1.1)
Задача (7.1.1) получила название задачи безусловной оптимизации, так как на изменения параметров состояния 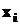 не накладывается никаких ограничений.
не накладывается никаких ограничений.
Следует отметить, что задача отыскания минимума очень легко может быть сведена к задаче на максимум и наоборот. Для этого необходимо ввести новую целевую функцию, связанную с исходной простым соотношением: 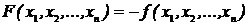 , тогда минимизация функции
, тогда минимизация функции 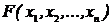 будет означать решение задачи об отыскании максимума функции
будет означать решение задачи об отыскании максимума функции 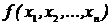 .
.
Но, к сожалению, изменение параметров 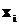 чаще всего не может быть совершенно произвольным, а должно подчиняться определенным законам, которые задаются в виде равенств или неравенств, что будет соответствовать задаче условной оптимизации, которая может быть записана в следующем виде:
чаще всего не может быть совершенно произвольным, а должно подчиняться определенным законам, которые задаются в виде равенств или неравенств, что будет соответствовать задаче условной оптимизации, которая может быть записана в следующем виде:


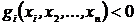 где i =1,2,…, k, (7.1.2)
где i =1,2,…, k, (7.1.2)

где k - количество ограничений в виде неравенств; l - количество ограничений в виде равенств. Задача (7.1.2) представляет собой обобщенную формулировку задачи математического программирования.
В зависимости от вида функций 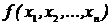 ,
, 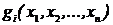 (где i = 1, 2,..., k) и
(где i = 1, 2,..., k) и  (где j =1, 2,..., l), задаваемых исходными условиями, принято осуществлять классификацию задач оптимизации.
(где j =1, 2,..., l), задаваемых исходными условиями, принято осуществлять классификацию задач оптимизации.
Если все функции в (7.1.2) линейны, то такая задача получила название задачи линейного программирования или сокращенно ЗЛП.
В том случае, когда хотя бы одна из этих функций является нелинейной, задача получила название задачи нелинейного программирования (НЛП). Наиболее простой нелинейной функцией является квадратичная, поэтому оптимизационные задачи, описываемые такими функциями, выделены в отдельный класс, называемый задачами квадратичного программирования.
Оптимизационные задачи, в которых переменные состояния  должны принимать только целые значения, составляют класс задач целочисленного программирования.
должны принимать только целые значения, составляют класс задач целочисленного программирования.
Когда целевая функция 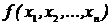 и ограничения
и ограничения 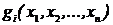 (где i= 1,2,..., k) и
(где i= 1,2,..., k) и  (где j= 1,2,..., l) представляются в виде позиномов вида
(где j= 1,2,..., l) представляются в виде позиномов вида 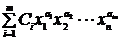 , то такая задача называется задачей геометрического программирования.
, то такая задача называется задачей геометрического программирования.
Важный класс задач оптимизации составляют задачи оптимального управления. Рассматривается система, состояние которой изменяется в моменты времени t= 1,2,..., N. Состояние системы определяется переменными состояния или фазовыми переменными, составляющими фазовый вектор или вектор состояний 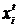 , где i= 1,2,..., n, а t= 1,2,..., N. Поведение системы может изменяться под воздействием совокупности управляющих переменных
, где i= 1,2,..., n, а t= 1,2,..., N. Поведение системы может изменяться под воздействием совокупности управляющих переменных 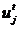 (где j= 1,2,...,r), называемых управлениями. Переход системы из одного состояния в другое описывается функцией
(где j= 1,2,...,r), называемых управлениями. Переход системы из одного состояния в другое описывается функцией  . Закон изменения состояния системы во времени, как правило, задается системой дифференциальных уравнений вида
. Закон изменения состояния системы во времени, как правило, задается системой дифференциальных уравнений вида 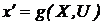 где
где  ,
, 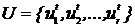 . Начальные значения фазовых переменных X при t =0, как правило, считаются заданными. Классификация задач оптимального управления осуществляется в зависимости от способа задания начальных значений фазовых переменных X. Когда при t =0 заданы значения всех фазовых переменных, задача оптимального управления получила название задачи со свободным правым концом; если же при t =0 задана только часть значений фазовых переменных, а недостающие компоненты заданы при t=N, то такая задача оптимального управления получила название задачи со скользящими концами.
. Начальные значения фазовых переменных X при t =0, как правило, считаются заданными. Классификация задач оптимального управления осуществляется в зависимости от способа задания начальных значений фазовых переменных X. Когда при t =0 заданы значения всех фазовых переменных, задача оптимального управления получила название задачи со свободным правым концом; если же при t =0 задана только часть значений фазовых переменных, а недостающие компоненты заданы при t=N, то такая задача оптимального управления получила название задачи со скользящими концами.
Качество функционирования системы оценивается критерием оптимальности вида 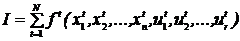 . Задача заключается в отыскании последовательности значений управляющих переменных U и соответствующих значений X (фазовой траектории), доставляющих критерию оптимальности экстремальное значение.
. Задача заключается в отыскании последовательности значений управляющих переменных U и соответствующих значений X (фазовой траектории), доставляющих критерию оптимальности экстремальное значение.
Особенности задач оптимального управления хорошо можно проследить на простейшем примере задачи о замене оборудования. Для простоты изложения ограничимся рассмотрением системы при двух временных интервалах, то есть N =2. В начальный момент времени система характеризуется состоянием эксплуатируемого оборудования, то есть его возрастом. В качестве критерия оптимальности принимаем затраты на содержание оборудования. Управляющая переменная U может принимать только два значения:  - сохранить оборудование;
- сохранить оборудование;  - заменить оборудование.
- заменить оборудование.
 X
X




 a
a  c
c


 d
d
 e
e
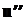

 b
b 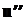 f
f

0 1 2 t
Рис.7.1.1
В начальный момент времени возможно принятие двух решений: заменить оборудование или оставить еще на один временной период. В зависимости от принятого на начальном этапе решения в момент времени t=1 система окажется в одном из двух состояний: a или b. В каждом из этих состояний также возможно принятие решения о замене оборудования. Это приводит к тому, что в момент времени t=2 система может находиться в одном из четырех состояний: a, b, e, f. Задача сводится к тому, чтобы из четырех возможных фазовых траекторий (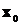 - a - c;
- a - c; 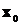 - a - d;
- a - d; 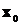 - b - e;
- b - e; 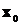 - b - f) выбрать ту, которая доставляет экстремальное значение для критерия оптимальности.
- b - f) выбрать ту, которая доставляет экстремальное значение для критерия оптимальности.
В задачах оптимального управления так же, как и в задачах математического программирования возможно присутствие ограничений на фазовые переменные в виде равенств и неравенств.
Таким образом, задачи оптимизации в общем случае представляют собой исследование некоторой функции на экстремум. Естественно, что наиболее старым методом решения будет являться использование дифференциальных свойств исследуемой функции, такой метод получил название классического. Но, к сожалению, оптимизационные задачи сложны и многообразны, а поэтому единого метода, позволяющего решать все задачи не существует. Этим и объясняется необходимость в проведении классификации задач оптимизации.
Для задач линейного программирования получены эффективные методы решения, ставшие практически стандартными. Задачи нелинейного программирования таких апробированных алгоритмов, к сожаления, не имеют, и требуется в каждом конкретном случае выбирать способ решения из достаточно большого количества методов, имеющихся в распоряжении исследователя.
Весьма интересной является разновидность задачи у которой множество возможных решений конечно и ограничено, хотя их число может быть и достаточно большим. Среди этого множества содержится и оптимальное. Такие задачи получили название задач комбинаторного программирования. Для их решения используются специальные методы.
Основным методом решения задач оптимального управления является метод динамического программирования, который может быть применен и к задачам нелинейного программирования в том случае, когда целевые функции этих задач удовлетворяют некоторым условиям, главным из которых является свойство аддитивности.
Если вы станете принимать решения так, как вам
подсказывает ваше сердце, то в результате вы
получите сердечную болезнь.
Х. Маккей
Не нашли, что искали? Воспользуйтесь поиском: